Методические рекомендации по теме: «Показатели вариации»

Первый блок заданий по данной теме – на знание (распознавание) формул расчета абсолютных и относительных показателей вариации:

Вариация – это изменение (колеблемость) значений признака в пределах изучаемой совокупности при переходе от одного объекта (группы объектов), или от одного случая к другому.

Абсолютные показатели вариации:

1) Размах вариации (R) представляет собой разность между максимальным (х_max) и минимальным (х_min) значениями признака в совокупности (в ряду распределения):

R = X_max - X_min. (1)

2) Среднее линейное отклонение вычисляется по следующим формулам:

по индивидуальным (несгруппированным) данным (2)	по вариационным рядам (сгруппированным данным) (3)
(2)	(3)

3) Дисперсия признака (s²) рассчитывается по формулам:

по индивидуальным (несгруппированным) данным (4)	по вариационным рядам (сгруппированным данным) (5)
(4)	(5)

4) Среднее квадратическое отклонение (s)представляет собой корень квадратный из дисперсии:

по индивидуальным (несгруппированным) данным (6)	по вариационным рядам (сгруппированным данным) (7)
(6)	(7)

Дисперсию можно определить и как разность между средним квадратом вариантов и квадратом их средней величины, т. е.

(8).

Относительные показатели вариации вычисляются как отношение ряда абсолютных показателей вариации к их средней арифметической и выражаются в процентах:

Коэффициент осцилляции		(9)
Коэффициент относительного линейного отклонения		(10)
Коэффициент вариации		(11)

Например,

Задача 1. Средняя заработная плата на одного рабочего в целом по группе предприятий составила 6 ден. ед. при дисперсии 0,81., средняя списочная численность рабочих составила 4000 при дисперсии 102 400. Тогда вариация заработной платы на одного рабочего:

а) больше вариации средней списочной численности рабочих;

б) меньше вариации средней списочной численности рабочих;

в) равна вариации средней списочной численности рабочих;

д) сравнивать вариацию названных показателей нельзя.

Решение

Рассчитаем показатели вариации по каждой совокупности:

1) коэффициент вариации средней заработной платы составит: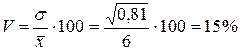

2) коэффициент вариации средней списочной численности рабочих составит:

Следовательно, вариации средней заработной платы рабочих больше, чем вариации средней списочной численности рабочих.