С помощью определения можно вычислять производные функций. Пример:
y= f(x)=x2 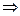 f(x+
f(x+ 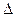 x)=(x+
x)=(x+ 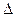 x)2=x2+2x
x)2=x2+2x 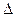 x+(
x+(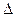 x)2
x)2 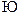
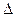 y= f(x+
y= f(x+ 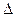 x) - f(x)=2x
x) - f(x)=2x 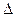 x+(
x+(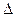 x)2.
x)2.
Отсюда 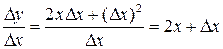 и
и 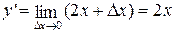 .
.
Совершенно аналогично можно получить и производные любых других функций. На этой основе разработана и постоянно используется стандартная таблица производных:
| у=С | 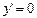 С - постоянная (число) С - постоянная (число) | |
| у=xa | 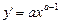 a a 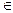 R R | |
| у=sin x | 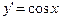 | |
| у=cos x | 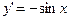 | |
| у=tg x | 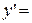 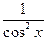 | |
| у=ctg x | 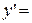 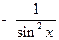 | |
| у=ax | 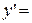 axln a axln a | |
| у=ex | 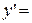 ex ex | |
| у=logax | 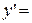 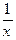 logae logae | |
| у=ln x | 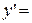 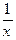 | |
| у=arcsin x | 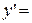 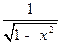 | |
| у= arccos x | 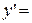 - - 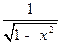 | |
| у=arctg x | 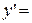 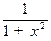 | |
| у=arcctg x | 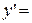 - - 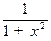 |
Теоремы дифференцирования
Так же, как и при вычислении пределов, математика разработала ряд теорем, ускоряющих вычислительную работу. Приведем их без доказательств:
1. Сумма: у=u(x) 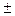 v(x)
v(x) 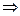
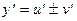 .
.
2. Произведение: y=u 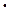 v
v 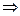
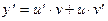 .
.
3. Частное: y= 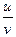

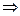
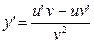 .
.
4. Постоянный множитель: y=Cu 
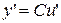 .
. 
 2015-10-22
2015-10-22 935
935








