Аргумент комплексного числа

Нехай вектор 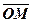зображає к.ч. 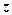, рис.1.5. Аргументом числа називається будь-яке із значень кута нахилу вектора 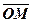до осі :

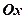, де .

Таким чином, аргумент к.ч. набуває нескінченну множину значень. Аргумент числа не визначається.

Рис. 1.5

Найменше за абсолютною величиною значення (тобто значення з інтервалу ) називається головним значенням аргументу к.ч. і позначається , тому , .

Приклади.

1) Використовуючи рис. 1.6, легко переконатись, що

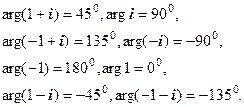
Рис. 1.6

2) Для довільного маємо . Пропонуємо довести цю тотожність самостійно.

Обчислення аргументу

Спочатку відмітимо властивість:

1) Аргумент дійсного і чисто уявного числа: якщо , то

2) Аргумент будь-якого числа можна знаходити за формулою:

(1.1)

Доведемо останню формулу у випадку, коли зображується точкою в другій чверті (рис.1.7). З . Оскільки , то

Рис 1.7

Інші випадки розміщення числа 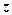на площині розглядаються аналогічно.

Зауважимо, що вказаним способом для аргументу можна одержати формули, в яких використовуються арккотангенс, арккосинус чи арксинус.

Якщо не вимагається високої точності, то аргумент к.ч. можна знаходити графічно. З цією метою слід побудувати к.ч. на міліметровому папері і виміряти відповідний кут за допомогою транспортиру. Цей спосіб іноді використовують для грубої перевірки обчислень.

Приклад 1. Покажемо, як обчислюють аргументи чисел за допомогою формул цього пункту.