Tpигонометрична форма к.ч

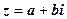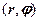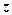Нехай відомі модуль і аргумент к.ч. (див рис.1.5). Зауважимо, що - полярні координати точки , яка зображає число (якщо 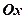- полярна вісь).

У випадку розміщення осей 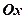і 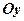, вказаному на рис. 1.5, відомі формули переходу від полярних до прямокутних координат точки 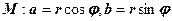. Додамо ці рівності, помноживши другу на :

Остання форма запису комплексного числа називається тригонометричною. Як бачимо, щоб знайти тригонометричну форму, досить обчислити модуль і аргумент к.ч.

Приклади. Записати в тригонометричній формі слідуючі числа:

1) 2) 3)

Розв’язання

1)

Відповідь:

2)

Відповідь:

3)

Відповідь: .

Розглянемо алгоритм переходу від алгебраїчної до тригонометричної форми к.ч.

Нехай дано к.ч. 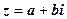, на прикладі . Для переходу до тригонометричної форми необхідно:

1. Побудувати на площині ХОУ к.ч. і встановити, до якої чверті належить . На даному прикладі: ІІІ четв. Див. рис.

2. Знаходимо модуль к.ч. 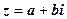за формулою (1)

(1)

На прикладі маємо:

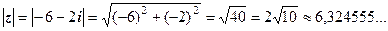
3. За допомогою таблиць або мікрокалькулятора знаходимо , ураховуючи при цьому властивість

.

На прикладі: .

4. За формулою (1.1) § 1.14 знаходимо . Для даного прикладу: ІІІ чверті. Маємо:

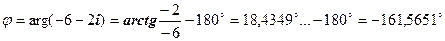
5. Підставимо знайдені і у формулу

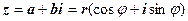(2)

Для маємо: