Нехай числа  записані в тригонометричній формі:
записані в тригонометричній формі:  .
.
Справедливі слідуючі формули:

Таким чином, при множенні (діленні) к.ч. їх модулі множаться (діляться), а аргументи додаються (віднімаються).
З’ясуємо геометричний зміст множення. Нехай 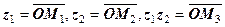 (рис 1.8). Очевидно, що
(рис 1.8). Очевидно, що 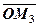 одержано поворотом
одержано поворотом  на кут
на кут  з подальшим розтягом (стиском)
з подальшим розтягом (стиском)  в
в  разів.
разів.
Отже, множення к.ч. зводиться до повороту і розтягу (стиску) векторів.
Подібний зміст має і ділення к.ч.

Рис.1.8
Приклад. Використовуючи тригонометричну форму, обчислити добуток чисел  З’ясувати геометричний зміст операції множення цих чисел.
З’ясувати геометричний зміст операції множення цих чисел.
Розв’язання. 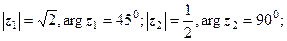

З геометричної точки зору були виконані слідуючі перетворення (рис.1.9):
1) поворот вектора 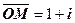 на кут
на кут  результат повороту;
результат повороту;
2) стиск (без зміни напряму) вектора  в 2 рази
в 2 рази  - результат множення.
- результат множення.
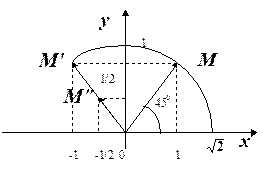
Рис.1.9
За допомогою рис.1.9 в даному випадку легко перевірити, що 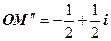 .
.
 2015-10-22
2015-10-22 338
338








