2015-10-22
8439
Задача 1.
Объем продукции u (ед), произведённый бригадой рабочих, может быть описан уравнением 
(ед), 
, где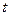 
-рабочее время, часы. Вычислить производительность труда, скорость и темп ее изменения через час после начала работы и за час до ее окончания.
Решение. Производительность труда выражается производной 
. Используя правило нахождения производной суммы функций – 
, получим
. Используя правила нахождения производной произведения постоянной на функцию: 
, производной степенной функции 
, производной константы: 
имеем:
(ед/ч)
Скорость изменения производительности – производная 
. Темп изменения производительности – логарифмическая производная 
(используем правило вычисления производной сложной функции, где 
)- сложная функция).
Найдем : 
(см. выше правила нахождения производной функции).
(ед/ч).
В заданные моменты времени 
и 
соответственно имеем:
( ед/ч ), 
(ед/ч ),
, 
,
(ед/ч), 
(ед/ч).
Итак, к концу работы производительность труда существенно снижается, при этом изменение знака и 
с плюса на минус свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня сменяется ее снижением в последние часы.
Задача 2. Найти дифференциал функции 
Решение. По определению 
(использовали правило нахождения сложной функции 
см. таблицу = 
).
