2015-10-22
318
Решить линейное дифференциальное уравнение первого порядка можно с помощью введения двух новых искомых функци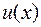й 
и 
, положив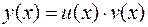 
, и дополнительного условия на одну из них, выбираемую произвольно. Рассмотрим применение этого метода на следующем примере.
Пример4. Решить дифференциальное уравнение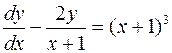 
.
Решение. Будем искать решение в виде: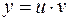 
;
Тогда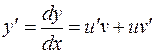 
; Подставляя выражения для искомой функции и ее производной в рассматриваемое дифференциальное уравнение, получим:
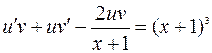, или
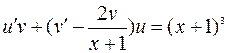. (7)
Поскольку одну из функци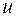й 
и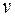 
мы вправе выбрать произвольно, выберем ее так, чтобы выполнялось условие: 
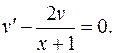Тогда уравнение (7) запишется в виде: 
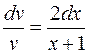. Это уравнение легко интегрируется: 
; 
.
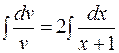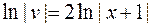Произвольную постоянную здесь можно положить равной нулю, так как мы выбираем частное решение. Тогда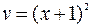 
.
После подстановки 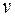в исходное уравнение получим (при 
):
; 
; 
.
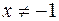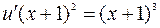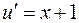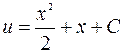Таким образом,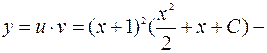 
искомое общее решение.
Уравнение Бернулли
Уравнением Бернулли называется уравнение следующего вида:
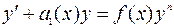. (8)
Здесь 
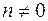и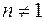 
, так как в этих случаях уравнение (8) превращается в линейное уравнение.
Уравнение Бернулли, как и линейное уравнение, решается с помощью представления этой функции в виде .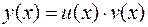
Пример5. Решить уравнение:
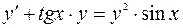. (9)
Решение. Это уравнение Бернулли и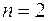 
. Положим 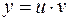. Тогда уравнение (9) запишется в виде:
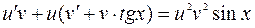. (10)
Будем искать функцию как решение уравнения:
.
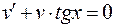Тогда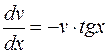 
и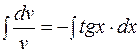 
. Вычисляя интегралы, получим:
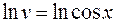и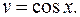 
Подставляя полученное выражение в (10), получим:
.
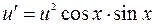Разделяя переменные и интегрируя, получим:
.
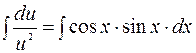Выполняя интегрирование, приходим к выражению:
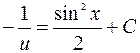, или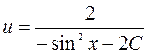 
.
Окончательно получаем: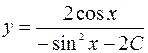 
.
Контрольные задания
а) Найти общее решение дифференциального уравнения.
б) Найти решение задачи Коши.
7.1. а)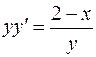 
;
б) 
;
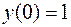7.2. а)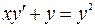 
;
б)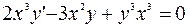 
; 
;
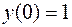7.3. а)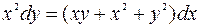 
;
б)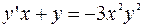 
; 
;
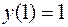7.4. а)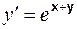 
;
б)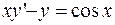 
; 
;
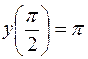7.5. а)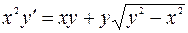 
;
б)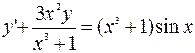 
; 
;
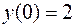7.6. а)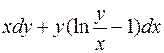 
;
б)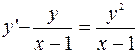 
; 
;
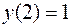7.7. а)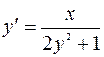 
;
б)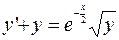 
; 
;
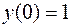7.8. а)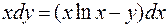 
;
б)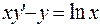 
; ;
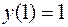7.9. а)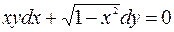 
;
б)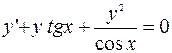 
; ;
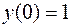7.10. а)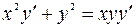 
;
б)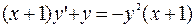 
; ;
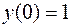7.11. а)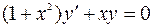 
;
б)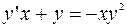 
; ;
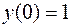7.12. а)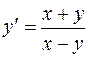 
;
б)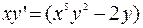 
; ;
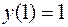7.13. а)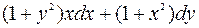 
;
б)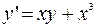 
; 
;
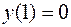7.14. а)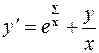 
;
б)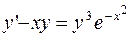 
; 
;
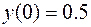7.15. а)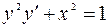 
;
б)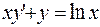 
; 
;
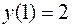7.16. а)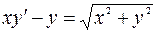 
;
б)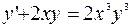 
; ;
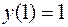7.17. а)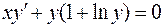 
;
б)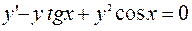 
; ;
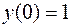7.18. а)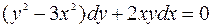 
;
б)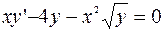 
; ;
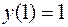7.19. а) 
;
б) 
; ;
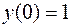7.20. а)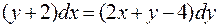 
;
б)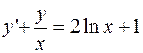 
; 
;
ТЕМА 8. РЯДЫ
