Пусть на отрезке [a, b] определена некоторая функция f(x). Будем говорить, что задано разбиение отрезка [a, b], если заданы точки x0,x1,...,xn, такие, что a = x0 < x1 <...< xn-1 <xn = b.
Разбиение отрезка [a, b] будем обозначать символом {xk}. Отрезки [xk-1,xk ], k = 1,...,n, называются частичными отрезками. Обозначим длины этих отрезков символами  :
: 
Диаметром разбиения называется число 
На каждом частичном отрезке выберем произвольным образом точку  и вычислим значение функции в этой точке
и вычислим значение функции в этой точке 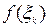 . По данному разбиению {xk} построим сумму:
. По данному разбиению {xk} построим сумму:  которая называется интегральной суммой или суммой Римана.
которая называется интегральной суммой или суммой Римана.
Функция f(x) называется интегрируемой (по Риману) на отрезке [a,b], если для любого разбиения {xk}, для которого  , и для любого выбора точек
, и для любого выбора точек  существует предел последовательности интегральных сумм
существует предел последовательности интегральных сумм  и он равен А:
и он равен А: 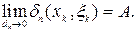
В этом случае число А называется определенным интегралом функции f(x) на отрезке [a,b] и обозначается 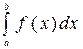 .
.
Рассмотрим геометрический смысл интегральной суммы в случае непрерывной неотрицательной функции 
Криволинейной трапецией назовем фигуру, ограниченную графиком функции y=f(x), прямыми x=a и x=b и отрезком [a,b] оси OX (Рис.4).

Рис. 4
Сделаем разбиение {xk} отрезка [a,b] и в каждом частичном отрезке [xk-1,xk] выберем точку  . Тогда каждое слагаемое интегральной суммы равно площади прямоугольника с основанием длины
. Тогда каждое слагаемое интегральной суммы равно площади прямоугольника с основанием длины  и высотой
и высотой  . Вся же сумма
. Вся же сумма  равна площади «ступенчатой фигуры», получающейся объединением всех указанных прямоугольников.
равна площади «ступенчатой фигуры», получающейся объединением всех указанных прямоугольников.
Из определения следует, что определенный интеграл  является пределом, при
является пределом, при  последовательности площадей соответствующих ступенчатых фигур, поэтому он равен площади криволинейной трапеции.
последовательности площадей соответствующих ступенчатых фигур, поэтому он равен площади криволинейной трапеции.
Можно доказать, что если функция y = f(x) непрерывна на отрезке [a,b], то она интегрируема на [a,b], т.е. предел интегральной суммы существует и не зависит от способа разбиения отрезка [a,b] на частичные отрезки [xk-1,xk] и выбора наших точек  .
.
Если функция f(x) интегрируема на отрезке [a,b], то ее интеграл является числом, не зависящим от обозначения переменной интегрирования: 
Для любой функции f(x), определенной в точке а, 
Для функции f(x), интегрируемой на [a,b], 
Свойства определенного интеграла
1. Если функции f(x) и g(x) интегрируемы на отрезке [a,b], то для любых вещественных чисел  справедливо равенство:
справедливо равенство:


2. Если функция f(x) интегрируема на отрезках [a,c] и [c,b], то она интегрируема и на отрезке [a,b], причем 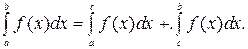
3. Если функция f(x) непрерывна на отрезке [a,b] и F(x) - какая-нибудь первообразная для f(x) на этом отрезке, то справедлива формула Ньютона-Лейбница:
 (1)
(1)
Символ 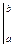 называется знаком двойной подстановки. С его помощью формула (1) записывается так:
называется знаком двойной подстановки. С его помощью формула (1) записывается так:
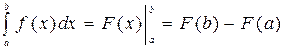
Пример 1. Вычислить следующие определенные интегралы по формуле (1):

Замена переменной и интегрирование по частям в определенном интеграле
Пусть функция f(x) непрерывна на отрезке [a,b], а функция  определена и непрерывна вместе со своей производной
определена и непрерывна вместе со своей производной  на отрезке
на отрезке  , причем
, причем  для любого
для любого  и
и  Тогда выполняется соотношение:
Тогда выполняется соотношение:
 (2)
(2)
Формула (2) называется формулой замены переменной в определенном интеграле.
Пример 2. Вычислить определенный интеграл  .
.
Сделаем замену переменной 
и пересчитаем пределы интегрирования: при x=1 t=1; при x=9 t=3.

Заметим, что при вычислении определенного интеграла по формуле (2) мы не возвращаемся к старой переменной.
Если функции U(x) и V(x) дифференцируемы на отрезке [a,b], то справедлива следующая формула интегрирования по частям:
 (3)
(3)
Пример 3. Вычислить интеграл  .
.
Применим формулу интегрирования по частям, обозначив:
 .
.
Тогда:

6.1-6.20. Вычислить определенные интегралы.
6.1 
6.2 
6.3 
6.4 
6.5 
6.6 
6.7 
6.8 
6.9 
6.10 
6.11 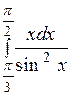
6.12 
6.13 
6.14 
6.15 
6.16 
6.17 
6.18 
6.19 
6.20  .
.
 2015-10-22
2015-10-22 1289
1289
