1.Понятие множества, подмножества. Понятие множества является одним из основных неопределяемых понятий математики.
Опр: Под множеством понимают совокупность (собрание, класс, семейство…) некоторых объектов, объединенных по какому-либо признаку. Так, можно говорить о множестве студентов колледжа, о множестве всех натуральных чисел и тд.
Опр: Объекты, из которых состоит множество, называют его элементами. Множества принято обозначать заглавными буквами латинского алфавита, например А, В,…, Х,…, а их элементы – малыми буквами а, в, … ,х,…
Если элемент х принадлежит множеству Х, то записывают  , запись
, запись 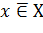 или
или  означает, что элемент х не принадлежит множеству Х.
означает, что элемент х не принадлежит множеству Х.
Опр: Множество, не содержащее ни одного элемента, называется пустым, обозначается символом  .
.
Опр: Множество называют конечным, если число его элементов конечно.
Опр: Множество, отличное от пустого и конечного называют бесконечным.
Элементы множества записывают в фигурных скобках, внутри которых они перечислены (если это возможно), либо указывается общее свойство, которым обладают все элементы данного множества.
Например, запись 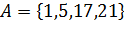 означает, что множество
означает, что множество  состоит из четырех чисел 1,5,17,21; запись
состоит из четырех чисел 1,5,17,21; запись  означает, что множество
означает, что множество  состоит из всех действительных чисел, удовлетворяющих неравенству
состоит из всех действительных чисел, удовлетворяющих неравенству 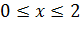 .
.
Опр: Множество  называют подмножеством множества
называют подмножеством множества  , если каждый элемент множества
, если каждый элемент множества  является элементом множества
является элементом множества  . Символически это обозначают так
. Символически это обозначают так  («
(« включено в
включено в  ») или
») или 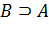 («множество
(«множество  включает в себя множество
включает в себя множество  »).
»).
Опр: Говорят, что множества  и
и  равны или совпадают, и пишут
равны или совпадают, и пишут 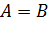 , если
, если  и
и  . Другими словами, множества, состоящие из одних и тех же элементов, называются равными.
. Другими словами, множества, состоящие из одних и тех же элементов, называются равными.
 1. Объединением (суммой) множеств
1. Объединением (суммой) множеств  и
и  называется множество
называется множество  , состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств. Объединение (сумму) множеств обозначают
, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств. Объединение (сумму) множеств обозначают  (или
(или 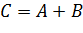 ). Кратко можно записать
). Кратко можно записать 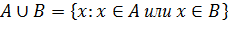 . Например: даны множества
. Например: даны множества  ,
,  , тогда
, тогда  .
.

 2. Пересечением (произведением) множеств
2. Пересечением (произведением) множеств  и
и  называется множество
называется множество  , состоящее из элементов, каждый из которых принадлежит множеству
, состоящее из элементов, каждый из которых принадлежит множеству  и множеству
и множеству  . Пересечение множеств обозначают
. Пересечение множеств обозначают  (или
(или 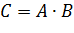 ). Кратко можно записать
). Кратко можно записать  . Например: даны множества
. Например: даны множества  ,
,  , тогда
, тогда  .
.
3. Разностью множеств  и
и  называется множество
называется множество  , состоящее из элементов множества
, состоящее из элементов множества  , не принадлежащих множеству
, не принадлежащих множеству  . Разность множеств обозначают
. Разность множеств обозначают 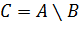 . Например: даны множества
. Например: даны множества  ,
,  , тогда
, тогда  .
.
 4.Дополнением множества
4.Дополнением множества  относительно множества
относительно множества  , называется множество
, называется множество  , если
, если  или
или 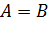 и СВ =В \ А. Например: даны множества
и СВ =В \ А. Например: даны множества  ,
, 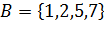 , тогда
, тогда  .
.
3. Пересечение и объединение. Для множеств  ,
,  и
и  справедливы следующие соотношения1.
справедливы следующие соотношения1. 
2.  – коммутативность объединения
– коммутативность объединения
3.  – ассоциативность объединения
– ассоциативность объединения
4. 
5. 
6.  – коммутативность пересечения
– коммутативность пересечения
7.  – ассоциативность объединения
– ассоциативность объединения
8. 
9. 
10. 
4. Некоторые логические символы. В дальнейшем для сокращения записей будем использовать некоторые логические символы:
 - символы включения.
- символы включения.  − «множество
− «множество  включено во множество
включено во множество  » или «множество
» или «множество  включает
включает  ».
».
 − «принадлежит»,
− «принадлежит»,  − «не принадлежит».
− «не принадлежит».
 − символ (квантор) общности, означает «для любого», «для всякого».
− символ (квантор) общности, означает «для любого», «для всякого».
 − символ (квантор) существования, означает «существует», «найдётся».
− символ (квантор) существования, означает «существует», «найдётся».
 − символ следствия. Запись
− символ следствия. Запись 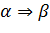 означает «из предложения
означает «из предложения  следует предложение
следует предложение  ».
».
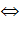 − символ равносильности (эквивалентности). Запись
− символ равносильности (эквивалентности). Запись  означает из
означает из  следует
следует  и из
и из  следует
следует  ».
».
 − союз «и»
− союз «и»
 − союз «или»
− союз «или»
: − «имеет место», «такое что».
 – означает отрицание предложения
– означает отрицание предложения  или «не
или «не  », черта над
», черта над  − символ отрицания.
− символ отрицания.
def − означает утверждение справедливо по определению.
Если несколько условий выполняется одновременно, то их объединяют знаком системы  , что соответствует союзу «и». Если же выполняется хотя бы одно из условий, то их объединяют знаком совокупности
, что соответствует союзу «и». Если же выполняется хотя бы одно из условий, то их объединяют знаком совокупности  , что соответствует союзу «или».
, что соответствует союзу «или».
Например: 1)  − для всякого элемента
− для всякого элемента 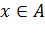 имеет место предложение
имеет место предложение  .
.
2)  − определение объединения множеств
− определение объединения множеств  и
и  .
.
3.1 Приведите примеры конечного и бесконечного множеств.
3.2 Даны множества  и
и  . Найти объединение, пересечение и разность множеств. Ответ:
. Найти объединение, пересечение и разность множеств. Ответ:  ,
,  ,
, 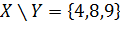 ,
, 
3.3 Даны множества  и
и  . Найти дополнение
. Найти дополнение 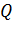 относительно
относительно  . Ответ:
. Ответ:  .
.
4. Обобщение урока (итоги, результаты).
5. Задание на дом. Разбор теоретического материала по конспектам лекций. Пример: Даны множества  и
и 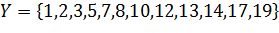 . Найти объединение, пересечение и разность множеств, дополнение
. Найти объединение, пересечение и разность множеств, дополнение 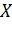 относительно
относительно 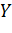 . Ответ:
. Ответ: 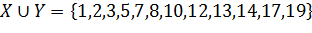 ,
, 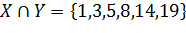 ,
, 

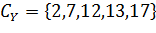 .
.
 2015-10-22
2015-10-22 2237
2237








