1) Предел многочлена. Для вычисления пределов многочлена f(х) = р(х) = ахп + вхп – 1 +… + с при х→а достаточно вместо переменной х подставить значение а, к которому она стремится, и выполнить соответствующие действия.
Пример3. Вычислить  Решение: Применим Теорему 1
Решение: Применим Теорему 1
 ) = 49
) = 49
2) Предел отношения двух многочленов 
а) если g(a) ≠ 0, то можно применить теорему о пределе частного.
Пример 4: Вычислить  =
=  .
.
б) если g(a) = 0, то теорему о пределе частного применить нельзя. Тогда если f(а) = А ≠ 0, то  = ∞.
= ∞.
Пример 5: 
в) если g(a) = 0 и f(а) = 0, то имеем неопределённость вида  . В этом случае предел
. В этом случае предел  можно вычислить разложением многочленов g(х) и f(х) на множители или заменой у = х – а.
можно вычислить разложением многочленов g(х) и f(х) на множители или заменой у = х – а.
Пример 6:
Вычислить 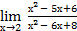 = (
= ( ) =
) =  =
=  =
=  или, заменяя у = х – 2 т.е. х = у + 2 и учитывая, что у→0 при х→2, получаем
или, заменяя у = х – 2 т.е. х = у + 2 и учитывая, что у→0 при х→2, получаем

 =
= 
 .
.
г) Если функция f(x) или g(x) содержит иррациональное выражение, в этом случае для вычисления предела, надо числитель и знаменатель умножить на выражение, сопряжённому корню.
Пример 7:
 =
=  =
=  =
=  =
=  =
=  = -
= - 
д) Если функция f(x) и g(x) содержит иррациональное выражение, в этом случае для вычисления предела, надо числитель и знаменатель умножить на выражение, сопряжённому корню числителя и знаменателя.
Пример 8:

Вычисление пределов в бесконечности. 
д) Если функция f(х) = ахn + bxn – 1 + … + c, то надо вынести за скобки хn, т.о.  f(x) =
f(x) = 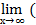 ахn + bxn – 1 + … + c) =
ахn + bxn – 1 + … + c) = 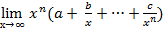 , тогда
, тогда  является бесконечно малой и стремится к 0.
является бесконечно малой и стремится к 0.
Пример 9: 
е) Если функция f(х) = 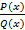 , где P(x) и Q(x) – многочлены n – степени, то при х →∞ числитель и знаменатель – величины бесконечно большие, поэтому получаем неопределённость вида
, где P(x) и Q(x) – многочлены n – степени, то при х →∞ числитель и знаменатель – величины бесконечно большие, поэтому получаем неопределённость вида  . Чтобы вычислить предел этой функции, надо числитель и знаменатель разделить на старшую степень знаменателя.
. Чтобы вычислить предел этой функции, надо числитель и знаменатель разделить на старшую степень знаменателя.
Пример 10:  = 0,6
= 0,6
Пример 11: 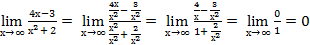
Пример 12: 
 2015-10-22
2015-10-22 2208
2208








