По данной теме ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Выполните упражнения для самопроверки.
Производная и ее приложения
Производная. Понятие производной является одним из фундаментальных понятий к математике. Многие задачи как самой математики, так и естествознания и техники приводят к этому понятию.
Пусть функция 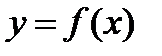 определена в промежутке
определена в промежутке 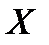 . Возьмем из этого промежутка фиксированное значение аргумента x и придадим ему приращение
. Возьмем из этого промежутка фиксированное значение аргумента x и придадим ему приращение 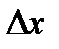 так, чтобы новое значение аргумента
так, чтобы новое значение аргумента 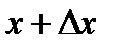 принадлежало этому промежутку. Тогда значение функции
принадлежало этому промежутку. Тогда значение функции 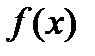 заменится новым значением
заменится новым значением 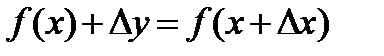 , т.е. функция получит приращение
, т.е. функция получит приращение 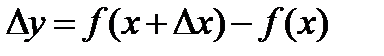 .
.
Предел отношения приращения функции 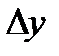 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента 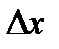 при стремлении
при стремлении 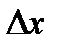 к нулю, т.е.
к нулю, т.е.
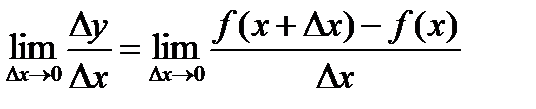 ,
,
называется производной функции 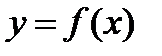 по аргументу x в точке x.
по аргументу x в точке x.
Производная обозначается одним из символов: 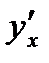 ,
, 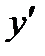 ,
, 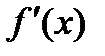 , а ее значение при
, а ее значение при 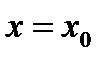 обозначается
обозначается 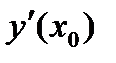 ,
, 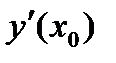 ,
, 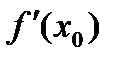 .
.
Операция нахождения производной называется дифференцированием.
Если функция 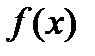 имеет производную в точке x, то она называется дифференцируемой в этой точке.
имеет производную в точке x, то она называется дифференцируемой в этой точке.
Если функция 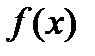 имеет производную в каждой точке промежутка X, то говорят, что эта функция дифференцируема на этом промежутке.
имеет производную в каждой точке промежутка X, то говорят, что эта функция дифференцируема на этом промежутке.
Производная сложной функции. Пусть 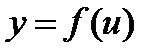 , где u является не независимой переменной, а функцией независимой переменной x:
, где u является не независимой переменной, а функцией независимой переменной x: 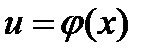 . Таким образом,
. Таким образом, 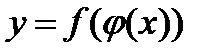 .
.
В этом случае функция y называется сложной функцией x, а переменная u – промежуточным аргументом.
Производная сложной функции находится на основании следующей теоремы: если 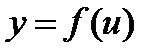 и
и 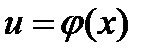 - дифференцируемые функции своих аргументов, то производная сложной функции
- дифференцируемые функции своих аргументов, то производная сложной функции 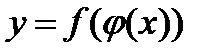 существует и равна произведению производной функции y по промежуточному аргументу и на производной промежуточного аргумента и по независимой переменной x:
существует и равна произведению производной функции y по промежуточному аргументу и на производной промежуточного аргумента и по независимой переменной x:
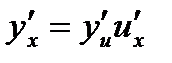 .
.
Эта теорема распространяется и на сложные функции, которые задаются с помощью цепочки, содержащей три звена и более.
Например, если 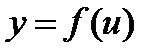 ,
, 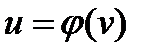 ,
, 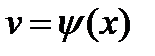 , т.е.
, т.е. 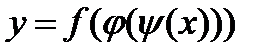 , то
, то 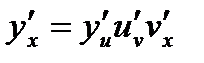 .
.
 2015-10-22
2015-10-22 684
684








