Характеристика методов интегрирования

Правило подведения под знак дифференциала.

Правило основано на следующем очевидном утверждении, которое следует из инвариантности формы первого дифференциала: если , где х – независимая переменная, то верно и равенство 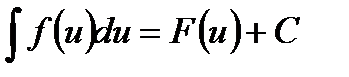, где u=u(x) – функция от х.

Например, ит.п.

На практике, исходный вид вычисленных интегралов обычно имеет другую форму: и сведение их к табличным интегралам обеспечивается равенством

То есть, используется таблица производных, прочитанная справа-налево. В первом случае под знак дифференциала внесли cosx, во-втором - .

Примеры.

. Здесь воспользовались

, так как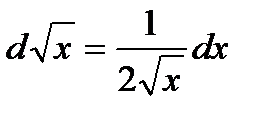

Следует отметить, что рассмотренное правило является частным случаем более общего правила замены переменной.