2015-10-22
347
Дифференциал произведения двух функци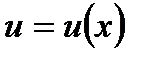й 
и 
определяется формулой 
. Перепишем равенство в виде 
и проинтегрируем обе части. С учетом свойств интеграла, получим формулу интегрирования по частям:
С помощью этой формулы обычно вычисляются интегралы от функций представляющих произведение многочлена на 
причем в первых трех случаях за 
обозначают многочлен, а в последнем 
. Поскольку в правой части формулы вместо функции 
появляется дифференциал этой функции 
, то есть возможность получить интеграл проще, если дифференциал функции проще, чем сама функция. После того как сама функция 
выбрана, оставшееся под интегралом выражение обозначаем 
, тогда сама функция 
.
Примеры.
a)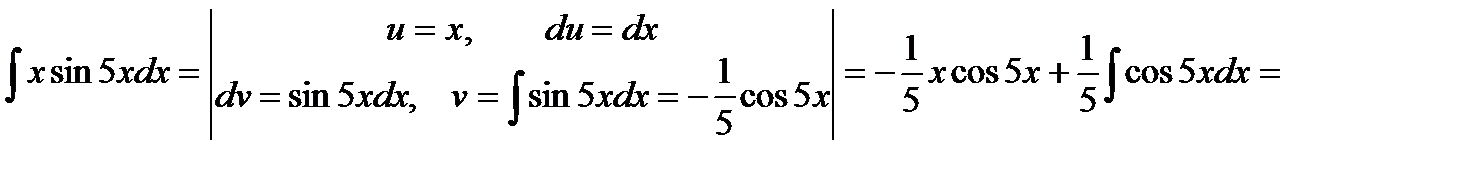 
b) 
