2014-02-09
2442
1.1. Коллинеарные векторы.
Теорема 3. Если векторы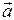 
и 
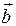коллинеарны, то существует единственное число 
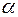такое, что
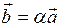, (1)
и наоборот.
∆ 
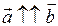, тогда 
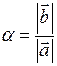; если 
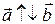, то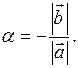 
Обратное очевидно. ▲
3.2..Компланарные векторы
Опр. Векторы, параллельные одной плоскости, называются компланарными.
Теорема 4. Если векторы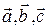 
компланарны и векторы 
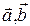неколлинеарны, то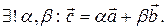 
∆ Отложим векторы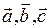 
от одной точки:
Проведем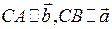 
. 
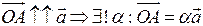(т.3)
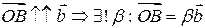(т.3). По правилу параллелограмма:
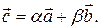
Допустим, что числа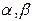 
не единственные: 
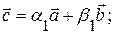вычитая, получим: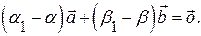 
Если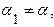 
то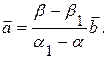 
Отсюда следует, что 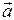и 
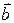
коллинеарны, что противоречит условию. Аналогично при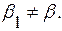 
▲
3.3. Линейная зависимость
Возьмем конечную систему векторов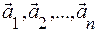 
и 
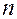чисел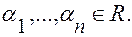 
Опр. Вектор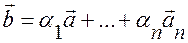 
называется линейной комбинацией векторов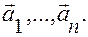 
!Опр. Векторы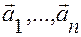 
называются линейно зависимыми, если существуют такие числа 
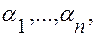не все равные нулю, что выполняется условие:
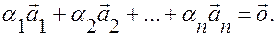(2)
Если равенство (2) выполняется только при нулевых коэффициентах, то векторы 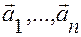называются линейно независимыми.
Теорема 5. (необх. и дост. условие л\зав.) Система векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов является линейной комбинацией остальных.
∆ 
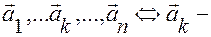л\к остальных.
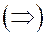Имеет место равенство (2). Пусть 
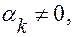тогда
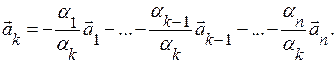
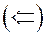очевидно ▲
3.4. Свойства линейных систем векторов
1. Если подсистема линейно зависима, то и вся система векторов л\з..
2. Если система л\нз, то любая её подсистема л\нз.
3. Всякая система, содержащая 0-вектор, линейно зависима.
Теорема 6. Два вектора л\з тогда и только тогда, когда они коллинеарны.
Теорема 7. Три вектора л\з тогда и только тогда, когда они компланарны.
