Лабораторная работа № 9

Наибольшее и наименьшее значения функции.
Исследование функций и построение их графиков

1. Цель работы

Приобретение умений исследовать функции с помощью дифференциального исчисления и строить их графики, в том числе и средствами программы MathCAD.

2. Содержание работы

1) Найдите наибольшее и наименьшее значения функции y = f (x) на отрезке [ a; b ] (табл. 1). Решение оформите в тетради.

2) Проведите полное исследование функции y = f (x) (табл. 2) и постройте ее график. Решение оформите в тетради и сдайте на проверку.

3) Используя программу MathCAD, постройте график функции y = f (x) (табл. 3). Выполненное задание отчитайте преподавателю.

3. Общие сведения и примеры выполнения заданий

ü Определение монотонных функций. Достаточные условия монотонности.

Пусть функция y = f (x) определена на интервале (a; b). Если для " х ₁, х ₂ Î (a; b), удовлетворяющих неравенству x ₁ < x ₂, выполняются условия:

1) f (x ₁) = f (x ₂), то y = f (x) называется постоянной на (a; b), т.е. y = C;

2) f (x ₁) < f (x ₂), то y = f (x) называется возрастающей на (a; b);

3) f (x ₁) £ f (x ₂), то y = f (x) называется неубывающей на (a; b);

4) f (x ₁) > f (x ₂), то y = f (x) называется убывающей на (a; b);

5) f (x ₁) ³ f (x ₂), то y = f (x) называется невозрастающей на (a; b);

Указанные в пунктах 1)-5) функции называются монотонными.

Теорема 1. (достаточные условия монотонности). Пусть функция y = f (x) дифференцируема на интервале (a; b). Тогда, если " х Î (a; b) выполняется условие:

1) 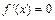, то f (x) постоянна на (a; b);

2) 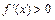, то f (x) возрастает на (a; b);

3) 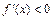, то f (x) убывает на (a; b).

ü Экстремум функции. Необходимые и достаточные условия экстремума.

Если при переходе через точку х ₀ слева направо функция изменяется от возрастания к убыванию, то точка х ₀ называется точкой максимума функции. Если же функция изменяется от убывания к возрастанию, то х ₀ называется точкой минимума. Точки максимума и минимума называются точками экстремума, а значение функции в точке экстремума называется экстремумом функции и обозначается символом f_max (x ₀) и f_min (x ₀).

Теорема 2. (необходимые условия экстремума). Для того, чтобы непрерывная функция y = f (x) имела экстремум в точке х ₀ необходимо, чтобы ее производная в этой точке равнялась нулю, т.е. 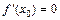или не существовала, т.е. .

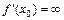Если выполняется 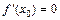, то точка х ₀ называется точкой гладкого экстремума. При 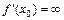точка х ₀ – точка острого экстремума.

Точки оси Ox, для которых выполняется теорема, называются критическими точками 1-го рода.

Наличие у функции критических точек 1-го рода, однако, не означает, что функция имеет в них экстремум. Поэтому нужно использовать достаточные признаки монотонности функции, позволяющие установить наличие экстремума и его характер (максимум или минимум).

Теорема 3. (достаточные условия экстремума). Если х ₀ – критическая точка 1-го рода функции y = f (x) и при переходе через нее слева направо производная меняет свой знак с плюса на минус, то х ₀ есть точка максимума, а если с минуса на плюс, то х ₀ – точка минимума.

ü Наибольшее и наименьшее значения функции.

Если функция y = f (x) непрерывна на отрезке [ a; b ], то по теореме Вейерштрасса она достигает на нем наибольшего и наименьшего значений. Это может произойти либо в точках экстремума, либо на концах отрезка. Поэтому для нахождения наибольшего и наименьшего значений на отрезке [ a; b ] рекомендуется пользоваться следующей схемой:

1. Найти производную .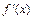

2. Найти критические точки 1-го рода, в которых 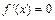или .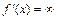

3. Найти значение функции в критических точках и на концах отрезка, затем выбрать из них наибольшее и наименьшее значения и записать их в ответ.

Пример 1. Найдите наибольшее и наименьшее значения функции 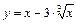на отрезке .

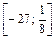Решение. 1) Находим производную: .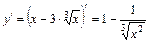

2) Находим критические точки, принадлежащие отрезку :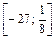

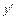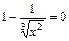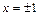а) производная равна нулю, т.е. , при , но ;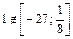

б) производная 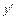не существует пр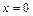и и .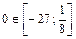

Вывод: получили две точки x = –1 и x = 0.

3) Вычисляем значения функции в критических точках и на концах отрезка:

, ,

, .

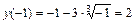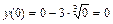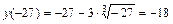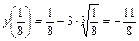Выбираем наибольшее и наименьшее значения: y _наим.(–27) = –18, y _наиб.(–1) = 2.

Ответ. y _наим.(–27) = –18, y _наиб.(–1) = 2.

ü Выпуклость и вогнутость графика функции. Точки перегиба.

Пусть функция y = f (x) на (a; b) имеет непрерывные производные 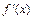и 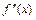. График дифференцируемой на интервале (a; b) функции y = f (x) называется выпуклым, если на этом интервале он расположен ниже любой своей касательной (рис. 1, а) и называется вогнутым, если он расположен выше любой своей касательной (рис. 1, б).

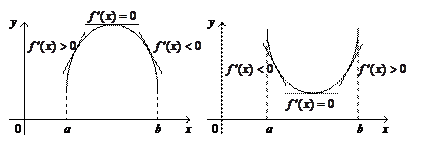а) б)

Рис. 1

Теорема 4. (достаточные условия выпуклости и вогнутости). График функции y = f (x) является выпуклым на (a; b), если 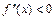, и является вогнутым на этом интервале, если .

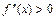Точка графика M ₀(x ₀; f (x ₀)) называется точкой перегиба, если в ней выпуклость графика функции меняется на вогнутость или наоборот.

Теорема 5. (необходимые условия существования точки перегиба). Пусть функция y = f (x) дважды дифференцируема на интервале (a; b) и в точке M ₀(x ₀; f (x ₀)) график имеет точку перегиба, тогда 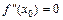или .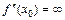

Точки оси Ox, для которых выполняется теорема, называются критическими точками 2-го рода.

Теорема 6. (достаточное условие существования точки перегиба). Пусть x ₀ Î (a; b) – критическая точка 2-го рода функции y = f (x). Тогда, если 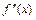меняет знак при переходе через точку х ₀, то M ₀(x ₀; f (x ₀)) есть точка перегиба.

ü Асимптоты графика функции.

Прямая линия называется асимптотой графика функции y = f (x), если расстояние от точки M (x; f (x)), лежащей на графике, до этой прямой стремится к нулю при движении точки M (x; f (x)) вдоль ветви графика в бесконечность.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

1) Прямая x = a называется вертикальной асимптотой графика функции y = f (x), если хотя бы один из односторонних пределов в точке a равен бесконечности, т. е. 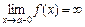или .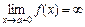

Очевидно, что график функции имеет вертикальную асимптоту x = a, если точка a есть точка разрыва 2-го рода или граничная точка области определения функции.

2) Прямая y = b называется горизонтальной асимптотой графика функции y = f (x), если существует конечный предел .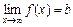

Если конечен лишь один из односторонних пределов 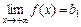или 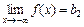, то график функции имеет соответственно правостороннюю y = b ₁ или левостороннюю y = b ₂ горизонтальную асимптоту. Если же b ₁ = b ₂, то асимптота называется двусторонней.

3) Прямая y = kx + b называется наклонной асимптотой графика функции y = f (x), если существуют конечные пределы 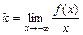, 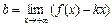или 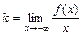, 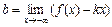соответственно.

В первом случае получается правосторонняя наклонная асимптота, во втором – левосторонняя. При совпадении этих пределов прямая y = kx + b является двусторонней наклонной асимптотой.

Горизонтальная асимптота является частным случаем наклонной асимптоты при k = 0. Поэтому если в каком-либо направлении график имеет горизонтальную асимптоту, то в этом направлении нет наклонной асимптоты, и наоборот.

ü Схема исследования функции и построения ее графика.

1. Найти область определения функции и указать ее точки разрыва, если они есть.

2. Выяснить, является ли функция четной, нечетной или общего вида.

3. Найти вертикальные асимптоты в точках разрыва функции и в граничных точках, и исследовать поведение функции вблизи вертикальных асимптот по односторонним пределам.

4. Исследовать поведение функции в бесконечности посредством нахождения горизонтальных и наклонных асимптот.

5. Найти производную 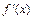, интервалы монотонности, точки экстремума и экстремумы функции.

6. Найти вторую производную 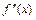, интервалы выпуклости и вогнутости графика функции, а также точки перегиба.

7. Найти точки пересечения графика с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.

8. На основании проведенного исследования построить график в следующей последовательности: а) построить асимптоты; б) изобразить экстремумы, точки перегиба и точки пересечения графика с осями координат; в) соединить указанные характерные точки гладкими кривыми с учетом интервалов монотонности функции, интервалов выпуклости и вогнутости графика и наличия асимптот.

Пример 2. Проведите полное исследование функции 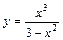и постройте ее график.

Решение. 1) Область определения функции – вся числовая прямая кроме точек 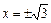, т. е. .

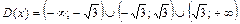Т. к. выполняется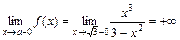

и 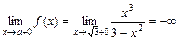, то точка 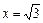является точкой разрыва 2-го рода. Аналогично, точка 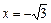так же является точкой разрыва второго рода, т. к. 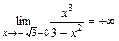и .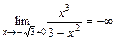

2) Т. к. на всей области определения функции выполняется 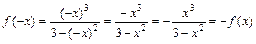, то функция является нечетной, следовательно, график функции симметричен относительно начала координат.

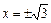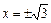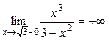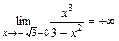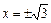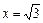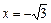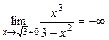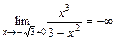3) Т. к. точки – точки разрыва 2-го рода, то прямые являются вертикальными асимптотами. Т. к. и , то при стремлении к точкам слева по оси абсцисс, график функции возрастает, неограниченно приближаясь к вертикальным асимптотам и соответственно. Т. к. и , то при стремлении к точкам 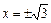справа по оси абсцисс, график функции стремиться вниз, неограниченно приближаясь к вертикальным асимптотам 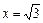и 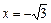соответственно.

4) Для нахождения горизонтальной асимптоты вычислим предел 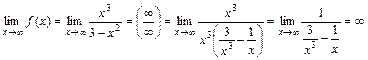, следовательно, горизонтальной асимптоты нет.

Наклонная асимптота задается уравнением y = kx + b.

Вычислим k и b:

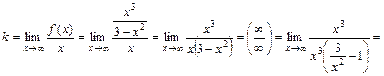
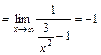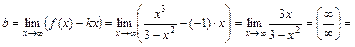
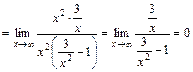Следовательно, прямая y = – x – наклонная асимптота.

5) Найдем первую производную функции:

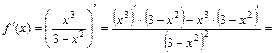
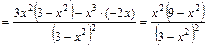Так как 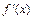не существует в точках 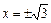, которые не принадлежит области определения функции, то критическими точками первого рода являются только точки, в которых 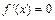или 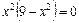, т. е. .

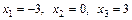Критические точки и точки разрыва 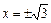разбивают числовую ось Ox на 6 интервалов монотонности функции. По знаку производной 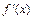в этих интервалах определяем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции. Полученные данные заносим в таблицу А.

Таблица А

x		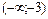–3		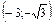		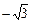		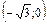		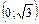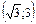(3;+¥)
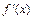	–		+	не сущ.	+	+	не сущ.	+		–
f (x)	m	4,5	k	не сущ.	k	k	не сущ.	k	–4,5	m
		min							max

6) Найдем вторую производную функции:

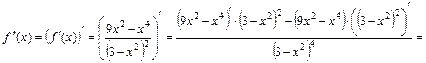
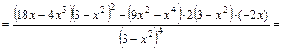
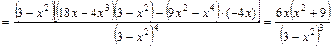Так как точки разрыва 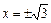не принадлежат области определения функции, то критическими точками второго рода являются точки, в которых 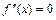, т.е. x = 0.

Критическая точка и точки разрыва разбивают числовую ось Ox на 4 интервала, в которых по знаку второй производной 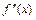определяем интервалы выпуклости и вогнутости графика и ординату точки перегиба. Полученные данные заносим в таблицу Б.

Таблица Б

x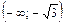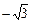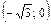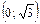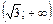
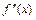	+	не сущ.	–		+	не сущ.	–
f (x)	È	не сущ.	Ç		È	не сущ.	Ç
				т.п.

7) Для нахождения точек пересечения графика с осью Ox решим уравнение 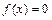или 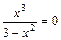, т.е. О (0; 0) – точка пересечения графика с осью абсцисс.

Для нахождения точек пересечения графика с осью Oy найдем значение функции при x = 0: 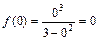, т.е. О (0; 0) – точка пересечения графика с осью ординат.

8) На основании проведенного исследования строим график в заданной последовательности (рис. 2).

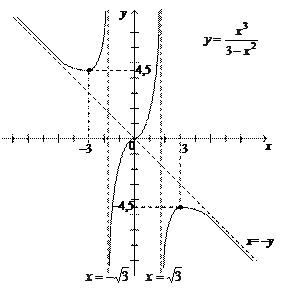Рис. 2

***

Настройка окон программы MathCAD для построения графиков функций в декартовой системе координат:

· На главной панели инструментов Math нажмите на кнопки и (если главной панели инструментов на экране нет, то V iew ® Toolbars ® M ath). Первая кнопка открывает панель Calculator, а вторая – панель Graph.

Для построения графиков функций в декартовой системе координат:

· Введите уравнение функции, используя, если нужно, панель Calculator. Например, 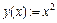. Знак присваивания «:=» вводится с клавиатуры нажатием комбинации клавиш Shift+«:».

· Нажмите на кнопку на панели Graph, которая используется для построения графиков функций в декартовой прямоугольной системе координат.

· В появившемся шаблоне заполните все поля как показано на рисунке.

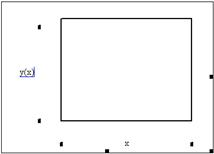
· Щелкните на свободном поле.

· При необходимости увеличьте размер рисунка, потянув мышкой за правый нижний уголок рамки.

· Изменяя вручную значения х и y можно получить график функции в «хорошем» качестве.

· Для получения на рисунке координатных осей двойным щелчком мыши по графику вызовите окно параметров Formatting Currently Selected Polar Plot и на вкладке X-Y Axes выберите стиль осей Crossed ® OK.

4. Индивидуальные задания

Таблица 1

№ вар.	y = f (x)	[ a; b ]	№ вар.	y = f (x)	[ a; b ]
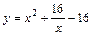		[1; 4]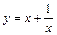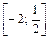
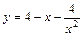		[1; 4]		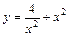	[1; 2]
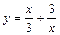		[1; 4]		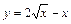	[0; 4]
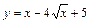		[1; 9]		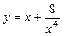	[1; 3]
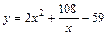		[2; 4]		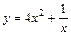	[–1; 1]
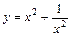		[1; 2]		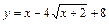	[–1; 7]
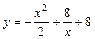		[–4; –1]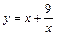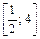
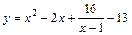		[2; 5]		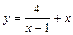	[–2; 0]

Продолжение табл. 1

№ вар.	y = f (x)	[ a; b ]	№ вар.	y = f (x)	[ a; b ]
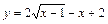		[1; 5]		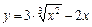	[0; 2]
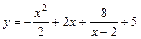		[–2; 1]		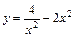	[–2; 2]
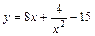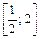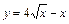					[0; 9]
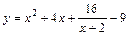		[–1; 2]		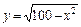	[–6; 8]
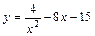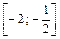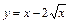					[0; 4]

Таблица 2

№ вар.	y = f (x)	№ вар.	y = f (x)	№ вар.	y = f (x)

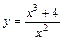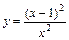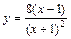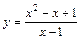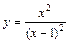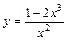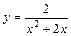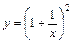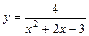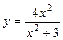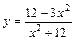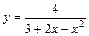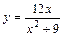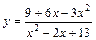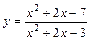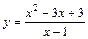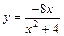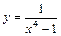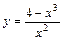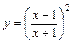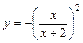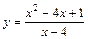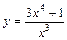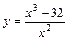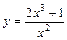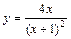Таблица 3

№ вар.	y = f (x)	№ вар.	y = f (x)	№ вар.	y = f (x)

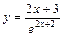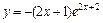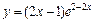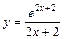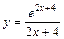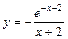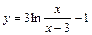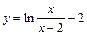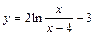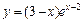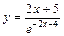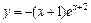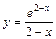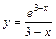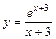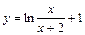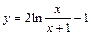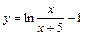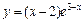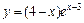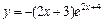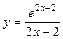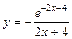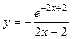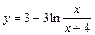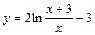Список литературы

1. Богородская, Т. Е. Лабораторный практикум по аналитической геометрии: методические указания к лабораторным работам для студентов 1 курса. Часть 1 / Т. Е. Богородская, Р. К. Катеринина, М. С. Хмелевская. – Волгоград: ВолгИСИ, 1992. – 24 с.

2. Богородская, Т. Е. Лабораторный практикум по аналитической геометрии: методические указания к лабораторным работам для студентов 1 курса. Часть 2 / Т. Е. Богородская, Р. К. Катеринина, М. С. Хмелевская. – Волгоград: ВолгИСИ, 1992. – 16 с.

3. Гурский, Г. А. Вычисления в Mathcad 12 / Г. А. Гурский, Е. С. Турбина. – СПб.: Питер, 2006. – 544 с.

4. Линьков, В. М. Высшая математика в примерах и задачах. Компьютерный практикум: учебное пособие / В. М. Линьков, Н. Н. Яремко / Под ред. А. А. Емельянова. – М.: Финансы и статистика, 2006. – 320 с.

5. Меркулов, В. А. Курс высшей математики. Избранные разделы. Разд. 1: Аналитическая геометрия: учебное пособие / ВолгГАСУ. – Волгоград, 2004. – 88 с.

6. Меркулов, В. А. Курс высшей математики. Избранные разделы. Разд. 2: Элементы линейной алгебры: учебное пособие / ВолгГАСУ. – Волгоград, 2004. – 64 с.

7. Меркулов, В. А. Курс высшей математики. Избранные разделы. Разд. 3: Введение в анализ: учебное пособие / ВолгГАСУ. – Волгоград, 2004. – 68 с.

План уч.-метод. докум. 2012 г., поз. № 4

Составители: Е. В. Абрамов, В. Н. Торопшина

Лабораторный практикум по математике
с информационной поддержкой
(использование программы MathCAD):
методические указания
по выполнению лабораторных работ
для студентов 1 курса
по направлению 270800.62 «Строительство»
(квалификация (степень) «бакалавр»)

Технический редактор Е. В. Румянцева

Подписано в печать 20.02.2012 г. Формат 60´84/16

Гарнитура Times New Roman. Бумага UNION PRINTS.

Печать трафаретная.

Усл. печ. л. 6,8. Уч.-изд. л. 7,3. Т. 35 экз.