2015-10-22
2323
Прямая на плоскости
1. Цель работы
Приобретение умений переходить от одного вида уравнения прямой к другому, строить прямые в декартовой прямоугольной системе координат, по рисунку записывать уравнение прямой.
2. Содержание работы
1) Запишите общее уравнение прямой (табл. 1, задание А) в виде:
– уравнения с угловым коэффициентом,
– уравнения в отрезках на осях,
– нормального уравнения.
Решение оформите в тетради.
2) По виду уравнений прямых (табл. 1) укажите особенности в расположении каждой прямой относительно осей координат и постройте эти прямые в декартовой прямоугольной системе координат. Решение оформите в тетради.
3) По эскизам (табл. 2) напишите уравнения изображенных прямых. Решение оформите в тетради и сдайте на проверку.
3. Общие сведения и примеры выполнения заданий
Углом наклона прямой к оси Ox называется угол a, образованный прямой с положительным направлением оси абсцисс (рис. 1).
Число k = tg a называется угловым коэффициентом прямой. Если a – острый, то k > 0, если a – тупой, то k < 0, если a = 0, то k = 0, если a – прямой, то k – не существует.
|
|
|
 |
Рис. 1
Различные виды уравнения прямой на плоскости.
1. Уравнение прямой, проходящей через заданную точку M 1(x 1; y 1) в данном направлении k:
y – y 1 = k (x – x 1). (1)
2. Уравнение прямой с угловым коэффициентом:
y = kx + b. (2)
| k > 0, b > 0 | k > 0, b < 0 | k < 0, b > 0 | k < 0, b < 0 |
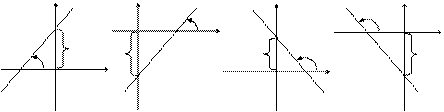a b
| a b | b a | a b |
| k > 0, b = 0 | k < 0, b = 0 | k = 0, b > 0 | k = 0, b < 0 |
a
| a | b | b |
3. Уравнение прямой, проходящей через две заданные точки M 1(x 1; y 1) и M 2(x 2; y 2):
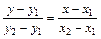. (3)
Угловой коэффициент прямой в этом случае:
. (4)
Если x 2 – x 1 = 0 в знаменателе формулы (3), то получим уравнение прямой, параллельной оси Oy:
x = x 1. (5)
Если y 2 – y 1 = 0 в формуле (3), то получим уравнение прямой, параллельной оси Ox:
y = y 1. (6)
4. Уравнение прямой в отрезках на осях:
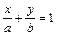. (7)
 a > 0, b > 0
| a > 0, b < 0 | a < 0, b > 0 | a < 0, b < 0 |
5. Нормальное уравнение прямой:
x cos a + y sin a – p = 0, (8)
где p = | ON | > 0, ON – отрезок, перпендикулярный прямой, называется нормалью; a – угол между нормалью и положительным направлением оси Ox (рис. 2).
Рис. 2
6. Общее уравнение прямой:
Ax + By + C =0, (9)
где хотя бы одно из чисел A или B не равно нулю. Числа А и В называются коэффициентами, а число С – свободным членом.
| A = 0 | B = 0 | C = 0 | A = 0, C = 0 | B = 0, C = 0 |
| By + С = 0 – прямая параллельна оси Oх | Ax + C = 0 – прямая параллельна оси Oу | Ax + By = 0 – прямая проходит через начало координат | By = 0 или y = 0 – прямая совпадает с осью Ox | Ax = 0 или x = 0 – прямая совпадает с осью Oy |
Пример 1. Запишите общее уравнение прямой 5 x + 3 y + 7 = 0 в виде: а) уравнения с угловым коэффициентом; б) уравнения в отрезках на осях; в) нормального уравнения.
|
|
|
Решение. а) Приведем уравнение 5 x + 3 y + 7 = 0 к виду (2). Для этого слагаемое с y перенесем вправо:
–3 y = 5 x + 7
и разделим на коэффициент при y:
.
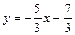Сравнивая полученное уравнение с (2), замечаем, что 
, 
.
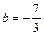б) Приведем общее уравнение к виду (7). Для этого свободный член перенесем вправо:
5 x + 3 y = –7
и обе части уравнения разделим на этот свободный член:
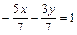или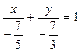 
.
Сравнивая полученное уравнение с (7), видим, что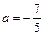 
, .
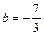в) Приведем уравнение 5 x + 3 y + 7 = 0 к виду (8). Для этого найдем число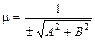 
, которое называется нормирующим множителем, где знак перед корнем в знаменателе выбирают противоположным знаку свободного члена С исходного уравнения Ax + By + C =0:
,
умножим теперь исходное уравнение на нормирующий множитель:
.
Сравнивая полученное уравнение с (8), очевидно, что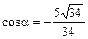 
, 
, 
.
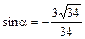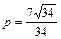Пример 2. Постройте прямые: а) 3 x – 2 y – 6 = 0; б) 2 x – 5 y = 0; в) 2 y – 1 = 0; г) 3 x + 2 = 0; д) 5 y = 0; е) 4 x = 0.
Решение. а) В уравнении 3 x – 2 y – 6 = 0 коэффициенты при x, y и свободный член не равны нулю. Геометрически такому уравнению соответствует прямая, пересекающая обе оси координат. Построить ее можно двумя способами: 1) по отрезкам на осях; 2) по точкам пересечения прямой с осями координат.
Способ 1. Приведем уравнение 3 x – 2 y – 6 = 0 к виду (7):
3 x – 2 y = 6 ®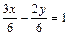 
® 
® 
.
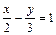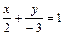Здесь a = 2, b = –3. Так как a = 2 > 0, то на оси Ox в положительном направлении от начала координат откладываем две единицы, а так как b = –3 < 0, то на оси Oy в отрицательном направлении от начала координат откладываем три единицы. Через полученные точки проводим искомую прямую (рис. 3).
 |
Рис. 3
Способ 2. Для построения прямой достаточно знать координаты каких-либо двух точек, например, точек пересечения прямой с осями координат. Полагая в данном уравнении x = 0, имеем:
–2 y – 6 = 0 ® 2 y = –6 ® y = –3.
Получаем А (0; –3) – точку пересечения прямой с осью Oy. При y = 0 находим:
3 x – 6 = 0 ® 3 x = 6 ® x = 2.
Точка В (2; 0) – точка пересечения прямой с осью Ox. По двум точкам А (0; –3) и В (2; 0) строим искомую прямую (рис. 3).
б) Прямая 2 x – 5 y = 0 проходит через начало координат О (0; 0), так как ее уравнение не содержит свободного члена. Для построения найдем еще одну точку на этой прямой. Пусть, например, х = 5, тогда из уравнения прямой 2 x – 5 y = 0 определим:
2 × 5 – 5 y = 0 ® 10 – 5 y = 0 ® 5 y = 10 ® y = 2
и получим точку E (5; 2). Через точки О (0; 0) и E (5; 2) проводим искомую прямую (рис. 4).
 |
Рис. 4
в) Прямая 2 y – 1 = 0 параллельна оси Ox, так как ее уравнение не содержит х. Из уравнения находим:
2 y = 1 ® 
и через точку 
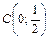параллельно оси Ox проводим искомую прямую (рис. 5).
Рис. 5
г) Так как в уравнении прямой 3 x + 2 = 0 отсутствует y, то прямая параллельна оси Oy. Из уравнения находим:
3 х = –2 ®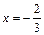 
и через точку 
параллельно оси Oy проводим искомую прямую (рис. 6).
 |
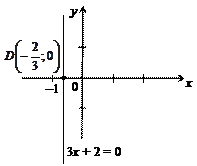Рис. 6
д) Прямая 5 y = 0 или y = 0 совпадает с осью Ox, так как в уравнении отсутствует х и свободный член.
е) Прямая 4 x = 0 или x = 0 совпадает с осью Oy, так как в уравнении отсутствует y и свободный член.
Пример 3. Напишите уравнения прямых, изображенных на рис. 7.
а) б)
в) г)
Рис. 7
Решение. а) На чертеже изображена прямая, которая отсекает отрезки от осей координат, поэтому ее уравнение будем искать в виде (7). Видно, что a = –3, b = 2. Подставим эти значения в (7):
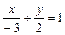
и после преобразований получим общее уравнение прямой:
2 x – 3 y + 6 = 0.
б) Прямая проходит через начало координат. Ее уравнение имеет вид:
Ax + By = 0. (*)
Найдем коэффициенты А и В. Точка М (1; 3) принадлежит этой прямой, поэтому ее координаты удовлетворяют уравнению (*):
A ×1 + B ×3 = 0,
откуда следует, что
А = –3 В. (**)
Подставим равенство (**) в уравнение (*):
–3 Вx + By = 0 ® – В (3 x – y) = 0.
Так как В ¹ 0, то, разделив на – В, получим искомое уравнение:
|
|
|
3 x – y = 0.
в) Прямая параллельна оси Ox, ее уравнение
y = – 2.
г) Прямая параллельна оси Oy, ее уравнение
x = 2.
Замечание. В примере 3 уравнения первых двух прямых можно получить и с помощью уравнения вида (3) прямой, проходящей через две заданные точки. В пункте а) известны координаты точек пересечения с осями координат, а в пункте б) это точки О и М.
4. Индивидуальные задания
Таблица 1
| № вар. | А) | Б) | В) | Г) |
| 2 х + 3 у – 6 = 0 | 7 х + 2 у = 0 | 6 у – 3 = 0 | 5 x + 15 = 0 | |
| 3 х – 4 у + 12 = 0 | 3 х – у = 0 | 2 х + 1 = 0 | 4 у – 6 = 0 | |
| 5 х + у – 7 = 0 | 3 х – 4 у = 0 | 3 х – 2 = 0 | 7 у – 8 = 0 | |
| х – 3 у + 5 = 0 | 2 х + 5 у = 0 | 2 х – 4 = 0 | 11 у – 6 = 0 | |
| 3 х + 6 у – 5 = 0 | 4 х + 3 у = 0 | 2 у – 7 = 0 | 10 х + 3 = 0 | |
| 2 х – у + 4 = 0 | 9 х + 2 у = 0 | 3 х – 1 = 0 | 8 у + 5 = 0 | |
| х – 5 у + 10 = 0 | 5 х – 9 у = 0 | 5 х – 6 = 0 | 11 у – 3 = 0 | |
| 2 х – 3 у – 7 = 0 | 2 х – 3 у = 0 | 3 у + 5 = 0 | 5 х + 2 = 0 | |
| 3 х – 4 у + 8 = 0 | 3 х – 8 у = 0 | 2 х + 3 = 0 | 6 у + 1 = 0 | |
| 9 х – 4 у + 36 = 0 | 2 х + 7 у = 0 | 4 х – 1 = 0 | 4 у – 3 = 0 | |
| х – 6 у + 12 = 0 | 2 х – 9 у = 0 | 5 х + 3 = 0 | 13 у + 4 = 0 |
Продолжение табл. 1
| № вар. | А) | Б) | В) | Г) |
| 2 х + 8 у – 9 = 0 | 3 х – 8 у = 0 | 8 х + 16 = 0 | 3 у – 5 = 0 | |
| 7 х – 4 у + 3 = 0 | 3 х + у = 0 | 3 у + 7 = 0 | 5 х + 3 = 0 | |
| 2 х – 3 у + 4 = 0 | 5 х – у = 0 | 12 у + 4 = 0 | 2 х + 7 = 0 | |
| 6 х + 5 у – 15 = 0 | 4 х – у = 0 | 6 у – 1 = 0 | 7 х + 5 = 0 | |
| х + 2 у + 6 = 0 | 7 х – 2 у = 0 | 3 у + 4 = 0 | 2 х + 11 = 0 | |
| 10 х + 3 у – 16 = 0 | 2 х + 15 у = 0 | 4 у – 7 = 0 | 2 х + 3 = 0 | |
| 3 х + 4 у – 7 = 0 | 3 х – 20 у = 0 | 15 у – 8 = 0 | 4 х + 7 = 0 | |
| 9 х – 4 у – 36 = 0 | 6 х + у = 0 | 7 у – 3 = 0 | 2 x + 1 = 0 | |
| 11 х + 2 у – 22 = 0 | 2 х + 15 у = 0 | 2 у – 13 = 0 | 3 х – 12 = 0 | |
| 3 х + 7 у – 2 = 0 | 4 х – 5 у = 0 | 8 у – 2 = 0 | 2 х – 1 = 0 | |
| 9 х – 5 у + 45 = 0 | 2 х – 3 у = 0 | 10 у – 7 = 0 | 8 х + 7 = 0 | |
| 12 х – 3 у + 24 = 0 | 8 х – 3 у = 0 | 3 у – 16 = 0 | 5 х + 1 = 0 | |
| 4 х + 7 у – 3 = 0 | 4 х – 5 у = 0 | 7 у – 2 = 0 | 11 х – 4 = 0 | |
| 5 х – у + 7 = 0 | 3 х + 4 у = 0 | 5 х + 2 = 0 | 9 y + 3 = 0 | |
| 3 х – 6 у + 5 = 0 | 6 х – 11 у = 0 | 3у – 1 = 0 | 2 x – 7 = 0 |
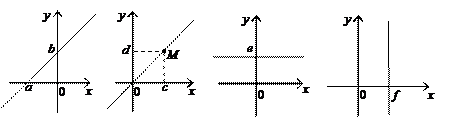Таблица 2
| № вар. | a | b | c | d | e | f |
| –3 | –5 | –1 | ||||
| –2 | –5 | –8 | ||||
| –7 | –1 | –2 | ||||
| –3 | –2 | –4 | ||||
| –4 | –3 | –4 | ||||
| –5 | –1 | –3 | ||||
| –2 | –2 | –5 | ||||
| –1 | –4 | –7 | ||||
| –2 | –8 | –7 | ||||
| –1 | –6 | –9 | ||||
| –8 | –4 | –3 | ||||
| –4 | –3 | –3 | ||||
| –8 | –5 | –6 | ||||
| –9 | –7 | –2 |
Продолжение табл. 2
|
|
|
| № вар. | a | b | c | d | e | f |
| –5 | –6 | –8 | ||||
| –9 | –6 | |||||
| –9 | –7 | –2 | ||||
| –6 | –5 | –5 | ||||
| –6 | –9 | –4 | ||||
| –5 | –3 | –1 | ||||
| –4 | –8 | –9 | ||||
| –5 | –3 | –4 | ||||
| –2 | –6 | –5 | ||||
| –1 | –6 | –9 | ||||
| –7 | –9 | –3 | ||||
| –1 | –2 | –5 |
