Вычисление пределов функций.
Первый и второй замечательные пределы
1. Цель работы
Приобретение умений вычислять пределы функций, имеющие неопределенности вида  ,
,  , (¥ – ¥), включая первый и второй замечательные пределы, в том числе и средствами программы MathCAD.
, (¥ – ¥), включая первый и второй замечательные пределы, в том числе и средствами программы MathCAD.
2. Содержание работы
1) Вычислите пределы функций (табл. 1). Решение оформите в тетради.
2) Вычислите пределы функций (табл. 2), используя первый и второй замечательные пределы. Решение оформите в тетради и сдайте на проверку.
3) Используя программу MathCAD, вычислите пределы функций (табл. 3). Выполненное задание отчитайте преподавателю.
3. Общие сведения и примеры выполнения заданий
Постоянное число a называется пределом переменной x, если для любого сколь угодно малого числа d>0 можно указать такое значение х, что все последующие значения будут удовлетворять неравенству | x – a | < d. Обозначение: lim x = a или x ® a. (1)
Неравенство | x – a | < d перепишем в виде –d < x – a < d или a – d < x < a + d. Интервал (a – d; a + d) называется окрестностью точки x = a радиуса d.
Постоянное число l называется пределом функции y = f (x) при x ® a, если для всех значений х, достаточно близких к а, значение f (x) сколь угодно мало отличается от l. Обозначение:  или
или  . (2)
. (2)
Определение включает случаи, когда числа а и l будут заменены символами «¥», «–¥», «+¥».
В определении не требуется, чтобы функция y = f (x) была определена в самой точке x = a.
Если существует предел (2) и x < a, то его называют пределом слева и обозначают 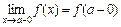 . (3) Аналогично, если существует предел (2) и x > a, то его называют пределом справа и обозначают
. (3) Аналогично, если существует предел (2) и x > a, то его называют пределом справа и обозначают  . (4)
. (4)
Пределы (3) и (4) называются односторонними пределами.
Если a = 0, то вместо x ® 0–0 и x ® 0+0 пишут соответственно x ® –0 и x ® +0.
Связь односторонних пределов с пределом (2) выражается следующей теоремой: для того, чтобы существовал предел (2) необходимо и достаточно, чтобы выполнялось f (a –0) = f (a +0).
Пусть функция y = f (x) определена в некоторой окрестности точки x = х 0, кроме, быть может, самой точки х 0. Функция y = f (x) называется бесконечно малой при x ® х 0, если  и называется бесконечно большой при x ® х 0, если
и называется бесконечно большой при x ® х 0, если  .
.
Здесь и в дальнейшем под символом х 0 подразумевается либо точка а либо ¥. Аналогично определяются бесконечно малые и бесконечно большие функции в случае односторонних пределов.
Если a(x) – бесконечно малая функция при x ® х 0 и a(x) ¹ 0 при x ¹ х 0, то обратная величина 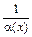 есть бесконечно большая функция при x ® х 0. И наоборот, если a(x) – бесконечно большая, то
есть бесконечно большая функция при x ® х 0. И наоборот, если a(x) – бесконечно большая, то 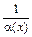 – бесконечно малая функция.
– бесконечно малая функция.
При решении задач удобно пользоваться следующей символической записью. Пусть число a > 0, тогда  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Основные теоремы и следствия о пределах функций.
1.  , где C – const.
, где C – const.
2. 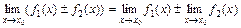 .
.
3.  .
.
4.  .
.
5.  , где C – const.
, где C – const.
6.  , где n – натуральное число.
, где n – натуральное число.
7.  , где Pn (x), Qm (x) – многочлены степени n и m соответственно и Qm (x 0)¹0.
, где Pn (x), Qm (x) – многочлены степени n и m соответственно и Qm (x 0)¹0.
Пример 1. Вычислите  .
.
Решение. Найдем значение функции  , стоящей в числителе, в точке х 0 = –1:
, стоящей в числителе, в точке х 0 = –1:  . Найдем значение функции
. Найдем значение функции  , стоящей в знаменателе, в точке х 0 = –1:
, стоящей в знаменателе, в точке х 0 = –1:  . Так как полученные значения конечны и отличны от нуля, то предел согласно утверждению 7 равен значению частного в предельной точке, т. е.
. Так как полученные значения конечны и отличны от нуля, то предел согласно утверждению 7 равен значению частного в предельной точке, т. е.  .
.
Ответ: 1,5.
8. Если существуют предел  и функция
и функция  , где n – натуральное число, то
, где n – натуральное число, то  .
.
9. Если существуют пределы  и
и  , то
, то  .
.
10. Пусть находится предел сложной функции y = f (j(x)) при x ® x 0. Тогда если существует  и существует
и существует  , то справедлива формула
, то справедлива формула  – правило замены переменной при нахождении предела сложной функции.
– правило замены переменной при нахождении предела сложной функции.
11. Если  и
и 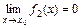 , то утверждение 4 применить нельзя и частное
, то утверждение 4 применить нельзя и частное  при x ® x 0 называется неопределенностью вида
при x ® x 0 называется неопределенностью вида  .
.
Пример 2. Вычислите  .
.
Решение. Подставим предельное значение х 0 = 3 в числитель и знаменатель дроби. Так как числитель и знаменатель оба равны нулю, то заданное отношение в точке  является неопределенностью вида
является неопределенностью вида  .
.
Для нахождения предела в этом случае:
1) Найдем корни уравнений 2 x 2 – 5 x – 3 = 0 и 3 x 2 – 4 x – 15 = 0.
   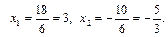 | ax 2 + bx + c = 0 D = b 2 – 4 ac,  , ,  |
2) Разложим квадратные трехчлены на линейные множители.
 , ,  | ax 2 + bx + c = a (x – x 1)(x – x 2) |
3) Сократим дробь на общий множитель  и найдем предел оставшегося выражения по утверждению 7:
и найдем предел оставшегося выражения по утверждению 7:
 .
.
Ответ: 0,5.
Пример 3. Вычислите  .
.
Решение. Значение числителя и знаменателя в точке х 0 = 2 равно нулю, следовательно, опять имеем неопределенность вида  .
.
Для нахождения предела в этом случае:
1) В числителе и в знаменателе выделим множитель х – 2, создающий неопределенность. С этой целью умножим числитель и знаменатель на выражение  сопряженное знаменателю и используем формулу сокращенного умножения (a – b)(a + b) = a 2 – b 2:
сопряженное знаменателю и используем формулу сокращенного умножения (a – b)(a + b) = a 2 – b 2:
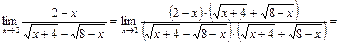

 .
.
2) Сократим дробь на множитель х – 2, получим:
 .
.
3) Вычисляя предел при х 0 = 2, окончательно получим:  .
.
Ответ:  .
.
12. Если  и
и  , то утверждение 4 применить нельзя и частное
, то утверждение 4 применить нельзя и частное  называется неопределенностью вида
называется неопределенностью вида  .
.
Пример 4. Вычислите:
а)  , б)
, б)  , в)
, в)  .
.
Решение. а) При х ® ¥ числитель и знаменатель стремятся к ¥, т. е. заданное отношение является неопределенностью вида  .
.
Для нахождения предела в этом случае:
1) В числителе и знаменателе вынесем за скобки старшую степень переменной х всей дроби (это х 3):
 и
и 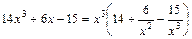 .
.
После сокращения дроби на х 3 применим утверждения 4, 2, 1, а также равенство  и получим:
и получим:
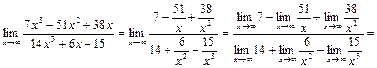
 .
.
б) При х ® ¥ заданное отношение так же является неопределенностью вида  . Повторим рассуждения, проделанные в пункте а). Выносим за скобки в числителе и знаменателе старшую степень переменной х всей дроби (это х 2), сокращаем дробь на х 2 и получаем:
. Повторим рассуждения, проделанные в пункте а). Выносим за скобки в числителе и знаменателе старшую степень переменной х всей дроби (это х 2), сокращаем дробь на х 2 и получаем:
 .
.
в) Проводим аналогичные рассуждения:

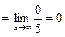 .
.
Ответ: а) 0,5, б) ∞, в) 0.
13. Если  и
и  , то утверждение 2 применить нельзя и разность f 1(x) – f 2(x) называется неопределенностью вида (¥ – ¥) при x ® x 0
, то утверждение 2 применить нельзя и разность f 1(x) – f 2(x) называется неопределенностью вида (¥ – ¥) при x ® x 0
Пример 5. Вычислите  .
.
Решение. Подстановкой предельного значения х 0 = 2 в выражение, стоящее под знаком предела, убеждаемся, что существует неопределенность вида (¥ – ¥).
Для нахождения предела в этом случае нужно разность записать в виде дроби, приведя к общему знаменателю, и упростить.

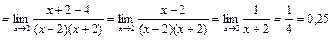 .
.
Ответ: 0,25.
Пример 6. Вычислите 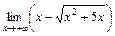 .
.
Решение. Опять имеем неопределенность вида (¥ – ¥).
Для вычисления предела снова нужно разность записать в виде дроби. С этой целью умножим числитель и знаменатель на выражение  сопряженное к числителю и используем формулу сокращенного умножения (a – b)(a + b)= a 2 – b 2.
сопряженное к числителю и используем формулу сокращенного умножения (a – b)(a + b)= a 2 – b 2.

 .
.
Теперь мы получили неопределенность вида  и нужно поступить аналогично примеру 4:
и нужно поступить аналогично примеру 4:

 .
.
Ответ: –2,5.
14. Если  и
и  , то утверждением 3 пользоваться нельзя и произведение f 1(x)× f 2(x) при x ® x 0 называется неопределенностью вида (0×¥).
, то утверждением 3 пользоваться нельзя и произведение f 1(x)× f 2(x) при x ® x 0 называется неопределенностью вида (0×¥).
Нахождение пределов для случаев 11-14 называется раскрытием неопределенности указанного вида.
Первый замечательный предел
Предел отношения синуса бесконечно малого угла к величине этого угла, выраженного в радианах, равен единице, т. е.  и называется первым замечательным пределом. Он используется для раскрытия неопределенностей вида
и называется первым замечательным пределом. Он используется для раскрытия неопределенностей вида  и (0×¥), содержащих тригонометрические и обратные тригонометрические функции.
и (0×¥), содержащих тригонометрические и обратные тригонометрические функции.
Пример 7. Вычислите 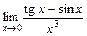 .
.
Решение. Заданное отношение в точке х 0 = 0 представляет неопределенность вида  . Вычислим этот предел, используя формулу первого замечательного предела, формулы тригонометрии и утверждения 3, 5, 10. С этой целью преобразуем выражение под знаком предела следующим образом:
. Вычислим этот предел, используя формулу первого замечательного предела, формулы тригонометрии и утверждения 3, 5, 10. С этой целью преобразуем выражение под знаком предела следующим образом:



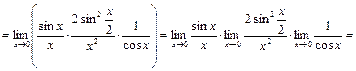

 .
.
Ответ: 0,5.
Пример 8. Вычислите  .
.
Решение. Выражение, стоящее под знаком предела, представляет собой неопределенность вида (0×¥) в точке х 0 = 0. Для решения воспользуемся формулой первого замечательного предела, формулами тригонометрии и утверждениями 3, 5, 10, 4 и 1. Преобразуем выражение под знаком предела следующим образом:
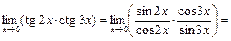

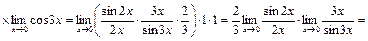

 .
.
Ответ:  .
.
Второй замечательный предел
Вторым замечательным пределом называется предел вида  . Он служит для раскрытия неопределенности вида (1¥).
. Он служит для раскрытия неопределенности вида (1¥).
Число е является бесконечной, непериодической дробью, приближенное значение которого равно е»2,718281828459045…»2,72.
С помощью замены переменной по формулам  ,
,  , t ® 0 при х ® ¥ второй замечательный предел можно представить в виде
, t ® 0 при х ® ¥ второй замечательный предел можно представить в виде  .
.
Пример 9. Вычислите  .
.
Решение. Воспользуемся вторым замечательным пределом, свойствами степеней и утверждениями 9, 10. С этой целью преобразуем выражение под знаком предела следующим образом:




 .
.
Указание: 
 .
.
Ответ:  .
.
Пример 10. Вычислите предел  .
.
Решение. Воспользуемся следствием из формулы второго замечательного предела  , а также свойствами степеней и правилами 6, 10:
, а также свойствами степеней и правилами 6, 10:
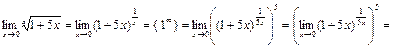
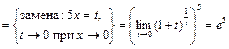 .
.
Ответ: е 5.
***
Настройка окон программы MathCAD для вычисления пределов функций:
· На главной панели инструментов Math нажмите на кнопки  и
и  (если главной панели инструментов на экране нет, то V iew ® Toolbars ® M ath). Первая кнопка открывает панель Calculator, а вторая – панель Calculus.
(если главной панели инструментов на экране нет, то V iew ® Toolbars ® M ath). Первая кнопка открывает панель Calculator, а вторая – панель Calculus.
Для вычисления предела функции:
· Выберите нужную кнопку  ,
,  или
или 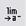 на панели Calculus. Первая кнопка используется для вычисления двустороннего предела, вторая – для предела справа, третья – для предела слева.
на панели Calculus. Первая кнопка используется для вычисления двустороннего предела, вторая – для предела справа, третья – для предела слева.
· В появившемся шаблоне заполните все поля, используя, если нужно, панель Calculator.
· Введите знак «®», набранный с клавиатуры с помощью комбинации клавиш Ctrl+«×» и щелкните на свободном поле.
Таблица 1
| № вар. | А) | Б) | В) |
 |  |  | |
 |  |  | |
 |  |  | |
 | 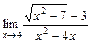 |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  |
Продолжение табл. 1
| № вар. | А) | Б) | В) |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
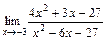 |  |  | |
 |  |  | |
 |  |  | |
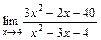 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
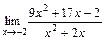 |  |  | |
 |  |  |
Таблица 2
| № вар. | А) | Б) |
 |  | |
 |  | |
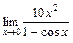 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
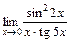 |  | |
 |  |
Продолжение табл. 2
| № вар. | А) | Б) |
 |  | |
 |  | |
 |  | |
 | 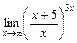 | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
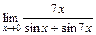 |  | |
 |  | |
 |  |
Таблица 3
| № вар. | Задание | № вар. | Задание |
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 | 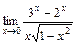 | ||
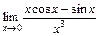 |  | ||
 |  | ||
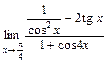 | 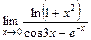 | ||
 |  | ||
 |  |
 2015-10-22
2015-10-22 1304
1304








