Кривые второго порядка

1. Цель работы

Приобретение умений построения кривых второго порядка в декартовой прямоугольной системе координат и составления их канонических уравнений.

2. Содержание работы

1) По виду уравнений (табл. 1) определите тип заданных кривых. Решение оформите в тетради.

2) Приведите уравнения кривых второго порядка (табл. 2) к каноническому виду и постройте их. Решение оформите в тетради.

3) Приведите уравнения кривых второго порядка (табл. 3) к каноническому виду и постройте их. Решение оформите в тетради.

4) Составьте каноническое уравнение: а) эллипса; б) гиперболы; в) параболы (табл. 4). Решение оформите в тетради и сдайте на проверку.

3. Общие сведения и примеры выполнения заданий

Уравнение второй степени с двумя неизвестными x и y вида

Ax ² + Bxy + Cy ² + Dx + Ey + F = 0, (1)

где хотя бы один из коэффициентов A, B, C отличен от нуля в декартовой прямоугольной системе координат может задавать: окружность, эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, пару совпадающих прямых, точку или пустое множество. Первые четыре линии называются кривыми второго порядка.

Если уравнение (1) не содержит произведение ху и имеет вид:

Ax ² + Cy ² + Dx + Ey + F = 0, (2)

то в зависимости от значений коэффициентов А и С по виду уравнения легко определить тип кривой:

а) если А × С > 0, то уравнение (2) задает линию эллиптического типа (эллипс, окружность, точку или пустое множество);

б) если А × С < 0, то уравнение (2) задает линию гиперболического типа (гиперболу или пару пересекающиеся прямые);

в) если А × С = 0, то уравнение (2) задает линию параболического типа (параболу, пару параллельных прямых, пару совпадающих прямые или пустое множество).

Пример 1. По виду уравнений определите тип заданных кривых:

а) х ² + 5 у ² – 3 х – 7 у – 7 = 0, б) 2 х ² – 3 у ² + 4 х – 5 = 0, в) 3 у ² – 2 х + 6 у = 0.

Решение. а) В уравнении А = 1, С = 5, следовательно, А × С > 0 и оно определяет линию эллиптического типа.

б) Из уравнения А = 2, С = –3, т.е. А × С < 0, а значит, это уравнение линии гиперболического типа.

в) В уравнении А = 0 и С = 3, т.е. А × С = 0. Заключаем, что дано уравнение параболического типа.

Вид кривой второго порядка не зависит от системы координат, поэтому для каждой кривой может быть выбрана такая система координат, в которой ее уравнение примет наиболее простой вид, называемый каноническим (простейшим).

Кривые второго порядка.

1. Окружность – это геометрическое место точек плоскости, равноудаленных от данной точки C (a; b) (центр окружности) на расстояние R (радиус окружности) (рис. 1). Каноническое уравнение:

(x – a)² + (y – b)² = R ². (3)

Рис. 1. Окружность (x – a)² + (y – b)² = R ²

В частном случае, а) если a = 0 (рис. 2, а), то каноническое уравнение окружности имеет вид:

x ² + (y – b)² = R ²; (4)

б) если b = 0 (рис. 2, б), то каноническое уравнение имеет вид:

(x – a)² + y ² = R ²; (5)

в) если a = b = 0 (рис. 2, в), то каноническое уравнение имеет вид:

x ² + y ² = R ². (6)

а) x ² + (y – b)² = R ² б) (x – a)² + y ² = R ² в) x ² + y ² = R ²

Рис. 2. Окружности

Пример 2. Определите тип линии x ² + y ² – 4 x + 8 y – 16 = 0 и постройте ее.

Решение. Сгруппируем все члены с х и отдельно с у:

(х ² – 4 х) + (у ² + 8 у) – 16 = 0.

Используя формулы (а ± b)² = a ² ± 2 ab + b ², выделим в первой скобке квадрат разности, а во второй – квадрат суммы и преобразуем:

(х ² – 2×2 х + 2² – 4) + (у ² + 2×4 у + 4² – 16) – 16 = 0,

(х – 2)² – 4 + (у + 4)² – 16 – 16 = 0,

(х – 2)² + (у + 4)² – 36 = 0,

(х – 2)² + (у + 4)² = 36.

Сравнивая полученное уравнение с уравнением вида (3) заключаем, что мы получили каноническое уравнение окружности с центром в точке С (2; –4) и радиусом R = 6. Строим линию (рис. 3).

Рис. 3

2. Пусть даны две точки F ₁ и F ₂, называемые фокусами, расстояние между которыми | F ₁ F ₂| = 2 c.

Эллипс – это геометрическое место точек плоскости, сумма расстояний от которых до фокусов есть величина постоянная, равная 2 а > 2 c.

Если фокусы взять в точках F ₁(– c; 0) и F ₂(c; 0), лежащих на оси Ох симметрично начала координат, то эллипс имеет вид как на рис. 4 и его каноническое уравнение есть:

, (7)

где

a > b, b ² = a ² – c ². (8)

Рис. 4. Эллипс

Точки А ₁(– а; 0), А ₂(а; 0), В ₁(0; – b), B ₂(0; b) называются вершинами эллипса, О (0; 0) – центр, отрезок | А ₁ А ₂| = 2 а называется большой осью, | B ₁ B ₂| = 2 b – малая ось, отрезки | А ₁ O | = | OA ₂| = а называются большими полуосями, | B ₁ О | = | OB ₂| = b – малые полуоси, отрезок | F ₁ F ₂| = 2 c называется межфокусным расстоянием, число – эксцентриситет эллипса, где 0 < e < 1 (определяет степень сжатия эллипса к оси Ох), числа r ₁ = a + e x, r ₂ = a – e x – фокальные радиусы точки М (x; y).

Более общим случаем эллипса (7) является эллипс (рис. 5) с центром в точке C (х ₀; у ₀), каноническое уравнение которого имеет вид:

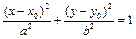(9)

Рис. 5. Эллипс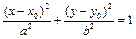

Пример 3. Определите тип линии и постройте ее:

а) 3 х ² + 4 у ² = 12; б) 4 х ² + 9 у ² – 16 х + 72 у + 124 = 0.

Решение. а) Приведем уравнение 3 х ² + 4 у ² = 12 к каноническому виду. Для этого обе части уравнения разделим на свободный член и преобразуем

3 х ² + 4 у ² = 12 ® ® ® .

По уравнению (7) устанавливаем, что дан эллипс (рис. 6, а). Осями симметрии эллипса служат оси координат, центр эллипса – точка О (0; 0), большая полуось а = 2, малая полуось , вершины эллипса – точки А ₁(–2; 0), А ₂(2; 0), , .

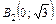б) Сгруппируем все члены с х и отдельно с у:

(4 х ² – 16 х) + (9 у ² + 72 у) + 124 = 0

и вынесем за скобки коэффициенты при х ² и у ²:

4(х ² – 4 х) + 9(у ² + 8 у) + 124 = 0.

Используя формулы (а ± b)² = a ² ± 2 ab + b ², выделим в скобках квадрат разности и квадрат суммы соответственно и преобразуем

4(х ² – 2×2 х + 2² – 4) + 9(у ² + 2×4 у + 4² – 16) + 124 = 0,

4((х – 2)² – 4) + 9((у + 4)² – 16) + 124 = 0,

4(х – 2)² – 16 + 9(у + 4)² – 144 + 124 = 0,

4(х – 2)² + 9(у + 4)² – 36 = 0,

4(х – 2)² + 9(у + 4)² = 36.

Делим обе части на свободный член в правой части:

® ® .

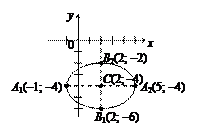
Согласно формулы (9) получаем каноническое уравнение эллипса (рис. 6, б) с центром в точке С (2; –4), оси симметрии – прямые х = 2 и у = –4, большая полуось а = 3 и малая полуось b = 2, вершины эллипса находятся в точках А ₁(–1; –4), А ₂(5; –4), В ₁(2; –6), В ₂(2; –2).

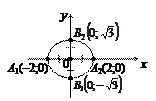а) б)

Рис. 6

Если фокусы располагать в точках F ₁(0; – c) и F ₂(0; c), лежащих на оси Оу симметрично начала координат или на прямой, параллельной этой оси, то соответствующие эллипсы будут задаваться так же формулами (7) и (9) и иметь вид как на рис. 7.

а) б)

Рис. 7. Эллипсы (7) и (9) соответственно

В этом случае a < b, a ² = b ² – c ², отрезок | B ₁ B ₂| = 2 b называется большой осью, | А ₁ А ₂| = 2 а – малая ось, – эксцентриситет эллипса, где 0 < e < 1 (определяет степень сжатия эллипса к оси Оy), числа r ₁ = b + e y, r ₂ = b – e y – фокальные радиусы точки М (x; y).

3. Пусть даны две точки F ₁ и F ₂, называемые фокусами, расстояние между которыми | F ₁ F ₂| = 2 c.

Гипербола – это геометрическое место точек плоскости, разность расстояний от которых до фокусов есть величина постоянная, равная ±2 а, где 2 а < 2 c.

Если фокусы взять в точках F ₁(– c; 0) и F ₂(c; 0), лежащих на оси Ох симметрично начала координат, то гипербола имеет вид как на рис. 8 и ее каноническое уравнение есть:

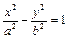, (10)

где

b ² = с ² – а ². (11)

Точки А ₁(– а; 0), А ₂(а; 0) называются вершинами гиперболы, О (0; 0) – центр, отрезок | А ₁ А ₂| = 2 а называется действительной осью, | B ₁ B ₂| = 2 b – мнимая ось, отрезки | А ₁ O | = | OA ₂| = а называются действительными полуосями, | B ₁ О | = | OB ₂| = b – мнимые полуоси, прямоугольник со сторонами 2 a и 2 b называется основным прямоугольником гиперболы, отрезок | F ₁ F ₂| = 2 c называется межфокусным расстоянием, число – эксцентриситет гиперболы, где e > 1 (определяет степень сжатия ветвей гиперболы к оси Ох), прямые – асимптоты гиперболы, для точек правой ветви гиперболы фокальные радиусы имеют вид r ₁ = a + e x и r ₂ = – a + e x, а для точек левой ветви – это r ₁ = – a – e x и r ₂ = a – e x.

Рис. 8. Гипербола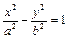

Если полуоси гиперболы (10) равны (a = b), то она называется равносторонней (рис. 9) и задается каноническим уравнением:

или x ² – y ² = a ². (12)

Рис. 9. Гипербола x ² – y ² = a

Эксцентриситет равносторонней гиперболы , ее асимптоты имеют уравнения y = ± x.

Более общим случаем гипербол вида (10) и (12) являются гиперболы (рис. 10) с центром в точке C (х ₀; у ₀), канонические уравнения которых имеет вид:

(13)

и

или (x – x ₀)² – (y – y ₀)² = a ². (14)

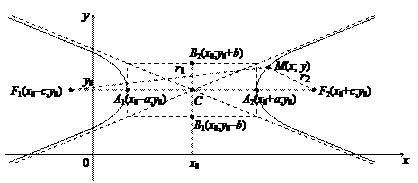
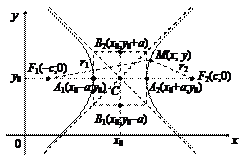а)

б)

Рис. 10. Гиперболы (13)–(14) соответственно

Пример 4. Определите тип линии и постройте ее:

а) 9 х ² – 4 у ² = 36; б) 4 х ² – 9 у ² – 8 х + 36 у – 68 = 0.

Решение. а) Приведем уравнение 9 х ² – 4 у ² = 36 к каноническому виду. Для этого обе части уравнения разделим на свободный член и преобразуем

9 х ² – 4 у ² = 36 ® ® ® .

Сравнивая полученное уравнением с формулой (10) делаем вывод, что дана гипербола. Оси симметрии гиперболы – оси координат, центр гиперболы – О (0; 0), действительная полуось а = 2, мнимая полуось b = 3, вершины находятся в точках А ₁(–2; 0) и А ₂(2; 0). Построение гиперболы начинаем с основного прямоугольника со сторонами 2 а = 4 и 2 b = 6, симметричного относительно начала координат и осей координат. Проводим диагонали прямоугольника и продолжаем их неограниченно в обе стороны. Они являются асимптотами гиперболы и имеют уравнения 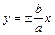, т.е. и . Затем строим гиперболу, которая пересекает ось Ox в своих вершинах и при удалении в бесконечность гипербола неограниченно приближается к асимптотам (рис. 11, а).

б) Выполним действия, аналогичные примеру 3, пункт б):

(4 х ² – 8 х) – (9 у ² – 36 у) – 68 = 0,

4(х ² – 2 х) – 9(у ² – 4 у) – 68 = 0,

4(х ² – 2 х + 1 – 1) – 9(у ² –4 у + 4 – 4) – 68 = 0,

4((х – 1)² – 1) – 9((у – 2)² – 4) – 68 = 0,

4(х – 1)² – 4 – 9(у – 2)² + 36 – 68 = 0,

4(х – 1)² – 9(у – 2)² – 36 = 0,

4(х – 1)² – 9(у – 2)² = 36,

® ® .

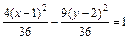Согласно формулы (13) получаем каноническое уравнение гиперболы с центром в точке С (1; 2), оси симметрии гиперболы – прямые х = 1 и у = 2, действительная полуось а = 3, мнимая полуось b = 2, вершины гиперболы находятся в точках А ₁(–2; 2), А ₂(4; 2). Основной прямоугольник имеет стороны 2 а = 6 и 2 b = 4, расположен симметрично относительно центра гиперболы и осей симметрии. Уравнения асимптот как прямых, проходящих через две заданные точки, можно получить, зная центр гиперболы и найдя координаты соответствующей вершины основного прямоугольника (рис. 11, б).

а) б)

Рис. 11

Если фокусы поместить в точки F ₁(0; – c) и F ₂(0; c), лежащие на оси Оу симметрично начала координат или на прямой, параллельной этой оси, то будут получаться гиперболы, аналогичные гиперболам (10), (12)-(14), имеющие вид как на рис. 12 и задаваться соответственно уравнениями:

, (15)

или у ² – х ² = b ², (16)

, (17)

или (y – y ₀)² – (x – x ₀)² = b ². (18)

а) в)

б) г)

Рис. 12. Гиперболы (15)-(18) соответственно

В этом случае точки B ₁ и B ₂ называются вершинами гиперболы, отрезок | B ₁ B ₂| = 2 b называется действительной осью, | А ₁ А ₂| = 2 а – мнимая ось, отрезки | B ₁ О | = | OB ₂| = b называются действительными полуосями, | А ₁ O | = | OA ₂| = а – мнимые полуоси, число – эксцентриситет гиперболы, где e > 1 (определяет степень сжатия ветвей гиперболы к оси Оy).

4. Параболой называется геометрическое место точек плоскости, одинаково удаленных от данной точки F, называемой фокусом и от прямой d, называемой директрисой. Расстояние от фокуса до директрисы называется параметром параболы и обозначается p, p > 0.

Если фокус взять и директрису , то получим параболу (рис. 13, а), каноническое уравнение которой имеет вид:

y ² = 2 px. (19)

Точка О (0; 0) называется вершиной параболы, ось Ох – осью симметрии параболы.

Если фокус и директрису выбирать тремя другими способами, то аналогично параболе (19) будем получать еще три параболы (рис. 13, б-г), канонические уравнения которых соответственно имеют вид:

y ² = –2 px, (20)

х ² = 2 pу, (21)

х ² = –2 pу. (22)

а) б)

в) г)

Рис. 13. Параболы (19)-(22) соответственно

Более общим случаем парабол (19)-(22) являются параболы (рис. 14) с центром в точке C (х ₀; у ₀), канонические уравнения которых соответственно имеет вид:

(y – у ₀)² = 2 p (x – х ₀), (23)

(y – у ₀)² = –2 p (x – х ₀), (24)

(х – х ₀)² = 2 p (у – у ₀), (25)

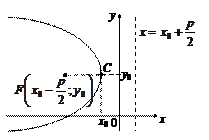(х – х ₀)² = –2 p (у – у ₀). (26)

а) б)

в) г)

Рис. 14. Параболы (23)-(26) соответственно

Пример 5. Определите тип линии и постройте ее:

а) ; б) у ² + 4 у – х + 5 = 0.

Решение. а) Сравнивая исходное уравнение

®

с уравнением (22), делаем вывод, что задано каноническое уравнение параболы 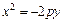, где . Ось симметрии параболы – ось Oy, вершина – начало координат, ее ветви направлены вниз. Фокус параболы находится в точке , т. е. , а ее директриса имеет уравнение , т. е. . Строим график (рис. 15, а).

б) Преобразуем левую часть уравнения, выделяя полный квадрат

(у ² + 4 у) – х + 5 = 0,

(у ² + 2×2 у + 2² – 4) – х + 5 = 0,

(у + 2)² – 4 – х + 5 = 0,

(у + 2)² – х + 1 = 0,

(у + 2)² = х – 1 ® .

Согласно формулы (23) получили параболу (рис. 15, б), вершина которой находится в точке С (1; –2), параметр , ось симметрии – прямая у = –2, ветви направлены вправо, фокус находится в точке 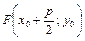, т. е. , а директриса задается уравнением , т. е. .

а) б)

Рис. 15

Пример 6. Составьте каноническое уравнение: а) эллипса, если левый фокус F ₁(–7; 0) и эксцентриситет ; б) гиперболы, если эксцентриситет e = 2 и точка М (; ) лежит на гиперболе; в) параболы, имеющей директрису х = –12.

Решение. а) По условию c = 7 и 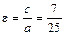, следовательно, a = 25. Найдем b ² = a ² – c ² = 625 – 49 = 576. Искомое уравнение эллипса .

б) Так как точка М (; ) принадлежит гиперболе , то имеем или 3 b ² – 2 a ² = a ² b ² (*). С другой стороны , следовательно, , откуда или . Подставляя это значение b в уравнение (*), получим, что , тогда находим . Искомое уравнение гиперболы .

в) Каноническое уравнение параболы в данном случае должно иметь вид у ² = 2 рх, ее фокус – в точке , а уравнение директрисы задается уравнением . По условию задачи уравнение директрисы х = –12, откуда находим , р = 24 и искомое уравнение параболы есть у ² = 48 х.

4. Индивидуальные задания

Таблица 1

№ вар.	Задание	№ вар.	Задание
	4 x 2 + 9 y 2 – 8 x – 36 y + 4 = 0 x 2 – 9 y 2 + 2 x + 36 y – 44 = 0 2 x 2 – 4 x + 2 y – 3 = 0		9 x 2 + 4 y 2 – 18 x – 8 y – 23 = 0 3 x 2 – 2 y 2 – 6 x + 4 y – 5 = 0 54 x 2 + 8 х – y + 7 = 0
	36 x 2 + 36 y 2 – 36 x – 24 y – 23 = 0 4 x 2 – 9 y 2 + 6 y – 1 = 0 x 2 – 2 x + 2 y – 3 = 0		4 x 2 + 9 y 2 + 16 x + 18 y – 11 = 0 3 x 2 – 2 y 2 + 6 x + 4 y – 5 = 0 у + 3 х 2 – 6 х + 5 = 0
	16 x 2 + 25 y 2 – 32 x + 50 y – 359 = 0 x 2 – y 2 – 6 x + 8 = 0 x 2 – 4 x – y – 3 = 0		y 2 + 2 x 2 + 4 x + 2 y + 1 = 0 2 x 2 – 2 y 2 + 4 x – 4 y – 2 = 0 x – y 2 – 3 y – 4 = 0
	x 2 + 4 y 2 – 8 y – 5 = 0 4 x 2 – 9 y 2 – 8 x + 36 y – 68 = 0 x 2 + 2 x + y + 3 = 0		2 x 2 + 2 y 2 + 4 x + 4 y + 2 = 0 3 x 2 + 6 x – 2 y 2 – 4 y – 5 = 0 х – 5 у 2 + 10 у – 6 = 0

Продолжение табл. 1

№ вар.	Задание	№ вар.	Задание
	x 2 + 9 y 2 + 2 x + 36 y + 1 = 0 36 x 2 – 36 y 2 – 72 x – 72 y – 1 = 0 4 x 2 – 2 x – y + 2 = 0		3 x 2 + 2 y 2 + 6 x + 4 y – 1 = 0 x 2 – 2 y 2 + 2 x – 4 y – 5 = 0 х + 2 у 2 – 8 у + 3 = 0
	9 x 2 + 4 y 2 – 36 x + 24 y – 36 = 0 x 2 – 4 y 2 – 8 y – 5 = 0 x + 2 y 2 – 4 y + 3 = 0		x 2 + 2 y 2 + 2 x + 4 y – 1 = 0 2 x 2 – y 2 + 4 x – 2 y – 1 = 0 х 2 – 2 х – 2 у + 1 = 0
	x 2 + y 2 + 6 x – 1 = 0 4 x 2 – y 2 – 8 x + 4 y – 1 = 0 2 x + y 2 – 2 y + 1 = 0		9 x 2 + 4 y 2 – 54 x – 32 y + 109 = 0 9 x 2 – 4 y 2 + 18 x + 18 y – 31 = 0 х 2 – 5 х – у + 7 = 0
	x 2 + y 2 – 6 x – 10 = 0 x 2 – 4 y 2 + 8 y – 5 = 0 3 x + y 2 – 2 y + 3 = 0		9 x 2 + 4 y 2 – 36 x + 24 y + 36 = 0 4 x 2 – 9 y 2 – 8 x = 32 у 2 + 2 х + 6 у – 1 = 0
	4 x 2 + 9 y 2 – 8 x – 36 y + 4 = 0 16 x 2 – 25 y 2 – 32 x + 50 y – 409 = 0 x + 2 y 2 – 6 y + 4 = 0		4 x 2 + 25 y 2 – 8 x + 96 = 0 4 x 2 – 9 y 2 + 16 x + 54 y – 101 = 0 у 2 + 6 у + 2 х + 19 = 0
	4 x 2 + 4 y 2 + 6 x + 4 = 0 9 x 2 – y 2 + 36 x + 2 y – 1 = 0 2 x + 2 y 2 + 4 y + 1 = 0		2 x 2 + 3 y 2 – 12 x + 6 y + 15 = 0 4 y 2 – 8 y – 9 x 2 – 32 = 0 х 2 – 6 х + 4 у + 9 = 0
	3 x 2 – 6 х + 2 y 2 – 4 y + 1 = 0 x 2 – y 2 + 2 y – 3 = 0 x 2 + 2 х – y + 4 = 0		9 x 2 + y 2 – 2 y + 10 = 0 x 2 + 2 х – 4 y 2 – 3 = 0 х 2 – 6 х + у + 10 = 0
	x 2 + y 2 – 6 x + 10 y – 15 = 0 4 x 2 – 9 y 2 – 8 x – 36 y – 68 = 0 2 x 2 + 8 х – y + 12 = 0		x 2 + 25 y 2 + 10 х = 0 9 x 2 – y 2 + 2 у – 10 = 0 у 2 + 6 у + 4 х + 13 = 0
	3 x 2 + 3 y 2 – 4 x + 9 y + 4 = 0 x 2 – 4 y 2 + 6 x + 16 y – 11 = 0 x 2 + 4 х – 6 y + 3 = 0		3 x 2 + 2 y 2 – 12 х – 4 у + 8 = 0 9 x 2 – 16 y 2 – 128 у – 112 = 0 у 2 + 6 у + 2 х + 4 = 0

Таблица 2

№ вар.	А)	Б)	В)
	16 х 2 + 3 у 2 = 48	х 2 – у 2 = 4	х 2 = –4 у
	9 х 2 + 25 у 2 = 225	х 2 – 18 у 2 = 35	у 2 = – х
	25 х 2 + 6 у 2 = 150	у 2 – х 2 = 9	у 2 = 3 х
	4 х 2 + 5 у 2 = 20	х 2 – 25 у 2 = 25	х 2 = –8 у
	9 х 2 + у 2 = 9	х 2 – у 2 = 16	х 2 = 9 у
	3 х 2 + у 2 = 3	у 2 – 10 х 2= 10	у 2 = 5 х
	16 х 2 + 5 у 2 = 80	9 у 2 – 4 х 2 = 36	у 2 = –8 х
	9 х 2 + 3 у 2 = 27	у 2 – х 2 = 16	х 2 = 14 у

Продолжение табл. 2

№ вар.	А)	Б)	В)
	25 х 2 + 7 у 2 = 175	4 х 2 – 16 у 2 = 64	х 2 = –15 у
	х 2 + у 2 = 5	у 2 – 4 х 2 = 4	у 2 = 8 х
	9 х 2 + 21 у 2 = 189	х 2 – 3 у 2 = 3	у 2 = –2 х
	х 2 + 5 у 2 = 5	у 2 – 6 х 2 = 6	2 х 2 = 3 у
	3 х 2 + 8 у 2 = 24	х 2 – у 2 = 1	7 х 2 = –2 у
	х 2 + 9 у 2 = 1	16 х 2 – 9 у 2 = 144	у 2 = 7 х
	25 х 2 + у 2 = 1	у 2 – х 2 = 9	у 2 = –9 х
	16 х 2 + 2 у 2 = 32	9 х 2 – 5 у 2 = 45	х 2 = –7 у
	9 х 2 + 4 у 2 = 36	5 х 2 – 4 у 2 = 20	х 2 = у
	16 х 2 + 9 у 2 = 144	у 2 – 5 х 2 = 5	у 2 = 5 х
	9 х 2 + 5 у 2 = 45	х 2 – у 2 = 16	у 2 = –4 х
	4 х 2 + у 2 = 4	4 у 2 – 15 х 2 = 60	х 2 = 6 у
	х 2 + 3 у 2 = 3	7 у 2 – 9 х 2 = 63	х 2 = – у
	16 х 2 + у 2 = 16	3 х 2 – 16 у 2 = 48	у 2 = 4 х
	5 х 2 + 9 у 2 = 45	7 х 2 – 16 у 2 = 112	у 2 = –7 х
	4 х 2 + 12 у 2 = 1	16 х 2 – у 2 = 64	2 х 2 = 5 у
	81 х 2 + 25 у 2 = 1	9 у 2 – х 2 = 81	3 х 2 = –4 у
	7 х 2 + у 2 = 7	4 х 2 – 13 у 2 = 52	3 у 2 = – х

Таблица 3

№ вар.	Задание	№ вар.	Задание
	9 х 2 + 4 у 2 – 54 х – 32 у + 109 = 0		2 х 2 + 5 у 2 + 8 х – 10 у – 17 = 0
	3 х 2 – 2 у 2 + 6 х + 4 у – 5 = 0		4 х 2 + 5 у 2 + 20 х – 30 у + 10 = 0
	2 х 2 – 2 у 2 + 4 х – 4 у – 2 = 0		9 х 2 + 9 у 2 + 42 х – 54 у – 95 = 0
	4 х 2 + 9 у 2 + 16 х + 18 у – 11 = 0		8 х 2 + 3 у 2 – 16 х + 12 у – 4 = 0
	9 х 2 + 4 у 2 – 18 х – 8 у – 23 = 0		6 х 2 – 4 у 2 + 36 х + 16 у + 2 = 0
	4 х 2 – 9 у 2 – 8 х + 36 у – 68 = 0		2 х 2 + 2 у 2 – 6 х + 10 у – 17 = 0
	3 х 2 + 3 у 2 – 6 х + 9 у + 4 = 0		5 х 2 + 9 у 2 – 30 х + 18 у + 9 = 0
	3 х 2 + 2 у 2 – 6 х – 4 у + 1 = 0		2 х 2 + 5 у 2 + 8 х – 10 у – 17 = 0
	36 х 2 – 36 у 2 – 72 х – 72 у – 1 = 0		16 х 2 – 9 у 2 – 64 х – 54 у – 161 = 0
	16 х 2 + 25 у 2 – 32 х + 50 у – 359 = 0		2 х 2 – 4 у 2 + 4 х – 8 у – 10 = 0
	4 х 2 + 9 у 2 – 8 х – 36 у + 4 = 0		4 х 2 + 2 у 2 + 8 х + 4 у – 2 = 0
	16 х 2 – 25 у 2 – 32 х + 50 у – 409 = 0		5 х 2 – 2 у 2 + 20 х + 4 у + 8 = 0
	4 х 2 + 9 у 2 + 32 х – 54 у + 109 = 0		7 х 2 + 9 у 2 + 14 х + 36 у – 20 = 0

Таблица 4

№ вар.	А)	Б)	В)
	b = 15, F 1(–10; 0)	a = 13,	d: x = –4
	A 2(4; 0),	b = 3,	d: y = –2
	a = 4, F 2(3; 0)	c = 5 ,	d: x = 2
	a = 11,	b = 2 , F 1(–11; 0)	d: y = –4
	b = 2, F 2(; 0)	a = 7,	d: x = 5
	A 1(–5; 0),	a = 8,	d: y = 1
	A 2(3; 0),	a = 5,	d: x = 6
	b = 4, F 2(9; 0)	b = ,	d: y = 4
	B 2(0; ),	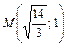a = 10,	d: x = 8
	A 2(8; 0),	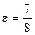b = 3, F 2(7; 0)	d: y = –1
	a = 12,	A 2(; 0), M (– ; 1)	d: x = –2
	b = 2,	a = 13,	d: y = 6
	a = 6, F 1(–4; 0)	c = 6,	d: x = 1
	A 2(8; 0),	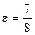b = 2, F 1(; 0)	d: y = 5
	b = 5,	c = 15,	d: x = 3
	a = 9, F 2(7; 0)	A 2(; 0),	d: y = 2

Продолжение табл. 4

№ вар.	А)	Б)	В)
	B 2(0; 8),	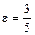a = 3,	d: x = 4
	b = 7, F 2(5; 0)	a = 11,	d: y = –3
	B 1(0; –2),	b = 6, F 2(12; 0)	d: x = –6
	A 1(–6; 0),	a = 6,	d: y = 8
	b = 5, F 1(–10; 0)	a = 9,	d: x = –5
	a = 25,	b = 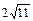, F 1(–7; 0)	d: y = 3
	b = ,	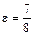A 2(; 0),	d: x = –1
	a = 13, F 1(–5; 0)	c = 9,	d: y = –6
	A 1(–3; 0),	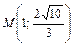b = 4, F 1(–11; 0)	d: x = –3
	b = 7, F 2(13; 0)	a = 6,	d: y = –5