Построение линий в полярной системе координат.
Построение на плоскости линий, заданных параметрически
1. Цель работы
Приобретение умений построения линий в полярной системе координат и линий, заданных параметрически, в том числе и средствами программы MathCAD.
2. Содержание работы
1) Постройте заданные точки в полярной системе координат (табл. 1). Решение оформите в тетради.
2) Определите вид кривых (табл. 2, задания А и Б) и постройте их в полярной системе координат. Решение оформите в тетради.
3) Определите вид кривой (табл. 3, задание А) и постройте ее в декартовой прямоугольной системе координат. Решение оформите в тетради и сдайте на проверку.
3) Используя программу MathCAD, постройте линию в полярной системе координат (табл. 2, задание В) и в декартовой прямоугольной системе координат (табл. 3, задание Б). Выполненное задание отчитайте преподавателю.
3. Общие сведения и примеры выполнения заданий
Зафиксируем на плоскости точку О и назовем ее полюсом. Из полюса проведем полуось Op, на которой выберем масштаб и назовем ее полярной полуосью. Такая совокупность называется полярной системой координат на плоскости.
 Положение произвольной точки М на плоскости однозначно определяется двумя числами: r =| OM |, называемое полярным радиусом точки М (
Положение произвольной точки М на плоскости однозначно определяется двумя числами: r =| OM |, называемое полярным радиусом точки М ( ) и j, называемое полярным углом точки М (
) и j, называемое полярным углом точки М (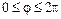 или
или 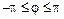 ) (рис. 1).
) (рис. 1).
Рис. 1
Числа r и j, взятые в указанной последовательности, называются полярными координатами точки М. Обозначение: М (r; j).
Полярный радиус точки О равен нулю, а ее полярный угол не определен.
На практике обычно приходится решать обратную задачу: по данным полярным координатам построить точку, причем в этом случае координаты не всегда удовлетворяют ограничениям для r и j. Если угол j принимает отрицательные значения, то он отсчитывается от полярной полуоси в отрицательном направлении (по часовой стрелке), а если его значение превышает по модулю 2p, то следует сделать нужное количество полных оборотов, чтобы упростить. Если r принимает отрицательные значения, то после поворота полярной полуоси на угол j для построения точки М надо отложить отрезок длиной | r | на продолжении полярной полуоси за полюс.
Пример 1. Постройте точки  ,
,  ,
, 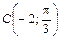 и
и  в полярной системе координат. Решение показано на рис. 2.
в полярной системе координат. Решение показано на рис. 2.
 |
Рис. 2
Для построения кривой, заданной в полярных координатах уравнением r = r (j), необходимо составить таблицу значений j и r в нескольких характерных точках, изучить поведение переменной r при переходе от одной точки к другой и соединить эти точки плавной линией.
Пример 2. Постройте кардиоиду  .
.
Решение. Так как полярный угол входит в уравнение только как аргумент тригонометрической функции косинус с периодом 2p, то достаточно рассмотреть значения j от 0 до 2p. Составим таблицу:
| j |  | 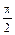 |  | p | |
| r | 1,7 | 0,3 | |||
| Точка | М 1 | М 2 | М 3 | М 4 | М 5 |
Нанесем полученные точки на чертеж (рис. 3).
 |
Рис. 3
Легко видеть, что при повороте полярного радиуса ОМ 1 против часовой стрелки точка М движется по нему, приближаясь к полюсу и последовательно занимая положения М 1, М 2, М 3, М 4, М 5. В силу четности функции косинус при повороте ОМ 1 по часовой стрелке движение точки М будет таким же. Соединяя точки плавной кривой, получаем кардиоиду  (рис. 4).
(рис. 4).

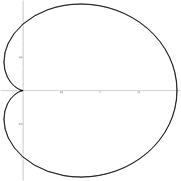
Рис. 4. Кардиоида 
Замечание. 1) Уравнения  ,
, 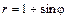 ,
,  также задают кардиоиду, но расположенную иначе (рис. 5).
также задают кардиоиду, но расположенную иначе (рис. 5).
 2) Уравнения
2) Уравнения  ,
,  , где а – некоторое число, задают кардиоиды аналогичные рис. 5.
, где а – некоторое число, задают кардиоиды аналогичные рис. 5.
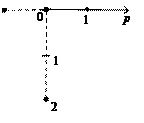




а)  б)
б) 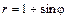 в)
в) 
Рис. 5. Кардиоиды
Пример 3. Постройте спираль Архимеда r = a j, где a > 0.
Решение. Составим таблицу:
| j |  | 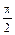 | p |  | 2p | |
| r | а  | а 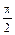 | а p | а  | а 2p | |
| Точка | О | М 1 | М 2 | М 3 | М 4 | М 5 |
Нанесем точки на чертеж и соединим их плавной линией (рис. 6).
 |

Рис. 6. Спираль Архимеда r = a j, a > 0
Ясно, что при дальнейшем повороте полярного радиуса ОМ точка М будет неограниченно удаляться по нему от полюса.
Пример 4. Постройте трехлепестковую розу 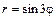 .
.
Решение. Составим таблицу:
| j |  |  | 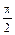 | 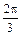 |  | p | |
| r | –1 | ||||||
| Точка | М 1 | М 2 | М 3 |
Если нанести на чертеж только эти точки, то непонятно, какой кривой их соединить. Изучим поведение функции r при изменении j от 0 до  . При этом sin 3j, а значит и r, монотонно растет от 0 до 1. Значит, при повороте полярного радиуса точка М удаляется по нему от точки О до точки М 1. При дальнейшем повороте точка приближается по полярному радиусу от М 1 к 0, затем переходит через точку О на продолжение полярного радиуса и удаляется до точки М 2, затем снова приближается до О и удаляется до М 3, снова возвращаясь к 0. Получаем кривую, изображенную на рис. 7, а.
. При этом sin 3j, а значит и r, монотонно растет от 0 до 1. Значит, при повороте полярного радиуса точка М удаляется по нему от точки О до точки М 1. При дальнейшем повороте точка приближается по полярному радиусу от М 1 к 0, затем переходит через точку О на продолжение полярного радиуса и удаляется до точки М 2, затем снова приближается до О и удаляется до М 3, снова возвращаясь к 0. Получаем кривую, изображенную на рис. 7, а.
Замечание. 1) Уравнение  также задает трехлепестковую розу, но повернутую на угол
также задает трехлепестковую розу, но повернутую на угол  по часовой стрелке (рис. 7, б).
по часовой стрелке (рис. 7, б).
2) Уравнения 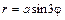 ,
,  , где а – некоторое число, задают трехлепестковые розы других размеров, но той же формы.
, где а – некоторое число, задают трехлепестковые розы других размеров, но той же формы.
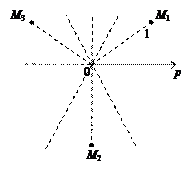 | |||
 | |||

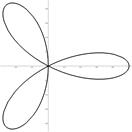
а) 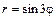 б)
б) 
Рис. 7. Трехлепестковые розы
Пример 5. Постройте четырехлепестковую розу: а) 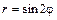 , б)
, б)  .
.
Решение показано на рис. 8. Точки М 1, М 2, М 3, М 4, М 5 соответствуют значениям  .
.
Замечание. Уравнения  ,
, 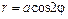 , где а – некоторое число, задают четырехлепестковые розы других размеров, но той же формы.
, где а – некоторое число, задают четырехлепестковые розы других размеров, но той же формы.
 | |||
 | |||


а) 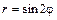 б)
б) 
Рис. 8. Четырехлепестковые розы
Пример 6. Постройте окружность  , где a > 0.
, где a > 0.
Решение. Составим таблицу:
| j |  |  |  | 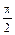 | 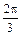 |  |  | p | |
| r | а |  |  |  | 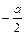 |  | 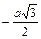 | – а | |
| Точка | М 1 | М 2 | М 3 | М 4 | М 5 | М 6 | М 7 | М 8 | М 9 |
 Соединяя точки плавной кривой, получаем окружность (рис. 9). Если придать аргументу j значения от p до 2p, то точка М пробегает эту окружность еще раз.
Соединяя точки плавной кривой, получаем окружность (рис. 9). Если придать аргументу j значения от p до 2p, то точка М пробегает эту окружность еще раз.

Рис. 9. Окружность  , где a > 0
, где a > 0
Замечание. Уравнения 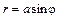 ,
,  ,
, 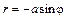 , где а > 0, задают окружности, показанные на рис. 10.
, где а > 0, задают окружности, показанные на рис. 10.




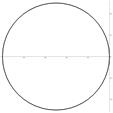

а) 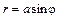 б)
б)  в)
в) 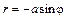
Рис. 10. Окружности
Функциональная зависимость между двумя величинами не всегда задается в явном виде формулой 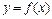 . Одним из видов неявного задания функции является параметрическое. В этом случае величины х и у задаются как некоторые функции параметра t:
. Одним из видов неявного задания функции является параметрическое. В этом случае величины х и у задаются как некоторые функции параметра t:  При этом каждому значению t 0 параметра t из общей области определения функций x (t) и y (t) соответствуют определенные значения x 0 = x (t 0) и y 0 = y (t 0).
При этом каждому значению t 0 параметра t из общей области определения функций x (t) и y (t) соответствуют определенные значения x 0 = x (t 0) и y 0 = y (t 0).
Для того, чтобы лучше понять, как задается эта функциональная зависимость, можно представить себе параметр t как время, а переменные х и у – как координаты движущейся точки М. При этом в момент времени t 0 точка М занимает положение M (x 0; y 0), где x 0 = x (t 0), y 0 = y (t 0).
Вообще говоря, параметр t может иметь совсем другой смысл, например, угла, длины дуги и т.д.
Для построения графика параметрически заданной функции надо найти значения x, y при некоторых фиксированных значениях параметра t и посмотреть, как меняются значения x и y.
Пример 7. Постройте астроиду 
Решение. Так как косинус и синус – периодические функции с периодом 2p, то достаточно построить график при t Î [0; 2p], т.к. при остальных значениях параметра t эта кривая будет проходиться точкой М повторно.
Пусть t 1 = 0, тогда x 1 = cos30 = 1, y 1 = sin30 = 0 и мы получим точку М 1(1; 0). При  имеем:
имеем:  ,
,  , М 2(0; 1). Как движется точка М при переходе от М 1 к М 2? Когда t меняется от 0 до
, М 2(0; 1). Как движется точка М при переходе от М 1 к М 2? Когда t меняется от 0 до 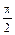 , то cos t (а вместе с ним и x = cos3 t) непрерывно уменьшается от 1 до 0, а sin t (а вместе с ним и y = sin3 t) непрерывно увеличивается от 0 до 1, т.е. точка М движется от М 1 влево и вверх к точке М 2 по непрерывной кривой. Для уточнения ее формы возьмем несколько значений
, то cos t (а вместе с ним и x = cos3 t) непрерывно уменьшается от 1 до 0, а sin t (а вместе с ним и y = sin3 t) непрерывно увеличивается от 0 до 1, т.е. точка М движется от М 1 влево и вверх к точке М 2 по непрерывной кривой. Для уточнения ее формы возьмем несколько значений  , нанесем соответствующие значения x и y на график и соединим их плавной линией. Аналогично построим оставшуюся часть астроиды (рис. 11).
, нанесем соответствующие значения x и y на график и соединим их плавной линией. Аналогично построим оставшуюся часть астроиды (рис. 11).
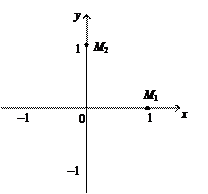

Рис. 11. Астроида 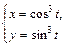
Замечание. Уравнения 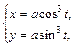 ,
,  где а, b > 0 – некоторые числа, задают астроиды других размеров. В первом случае форма сохраняется, а во втором случае астроида сжата к оси абсцисс, если a > b и сжата к оси ординат, если b > a.
где а, b > 0 – некоторые числа, задают астроиды других размеров. В первом случае форма сохраняется, а во втором случае астроида сжата к оси абсцисс, если a > b и сжата к оси ординат, если b > a.
Пример 8. Постройте циклоиду 
Решение. При t 1 = 0 получаем М 1(0; 0). При  получаем
получаем  . При t 3 = p получаем М 3(p; 2). Если t изменяется от 0 до
. При t 3 = p получаем М 3(p; 2). Если t изменяется от 0 до 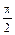 , то точка М переходит из М 1 в М 2, двигаясь вправо и вверх, а если t изменяется от
, то точка М переходит из М 1 в М 2, двигаясь вправо и вверх, а если t изменяется от 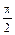 до p, то точка М переходит из М 2 в М 3, двигаясь вправо и вниз по непрерывной кривой. Для уточнения ее формы возьмем несколько значений t. Нанося полученные точки и соединяя их плавной линией, получим дугу, которая называется одной аркой циклоиды. Если продолжить строить точки, то получим общий вид циклоиды (рис. 12).
до p, то точка М переходит из М 2 в М 3, двигаясь вправо и вниз по непрерывной кривой. Для уточнения ее формы возьмем несколько значений t. Нанося полученные точки и соединяя их плавной линией, получим дугу, которая называется одной аркой циклоиды. Если продолжить строить точки, то получим общий вид циклоиды (рис. 12).
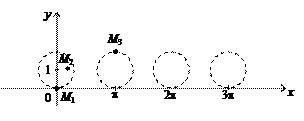

Рис. 12. Циклоида 
Указание. Уравнения  где а > 0 – некоторое число, задают циклоиду другого размера, но такой же формы.
где а > 0 – некоторое число, задают циклоиду другого размера, но такой же формы.
Пример 9. Постройте эллипс  где a, b > 0 – некоторые числа.
где a, b > 0 – некоторые числа.
Решение. Так как функции косинус и синус имеют период 2p, то достаточно построить график при t Î [0; 2p].
При t 1 = 0 получаем М 1(а; 0). При  получаем М 2(0; b). При изменении t от 0 до
получаем М 2(0; b). При изменении t от 0 до 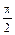 точка М переходит из М 1 в М 2, двигаясь влево и вверх по непрерывной кривой. Для уточнения ее формы возьмем несколько значений
точка М переходит из М 1 в М 2, двигаясь влево и вверх по непрерывной кривой. Для уточнения ее формы возьмем несколько значений  , нанесем соответствующие точки (x; y) на график и соединим их плавной линией. Аналогично рассуждая, достроим эллипс. При a > b эллипс сжимается к оси абсцисс (рис. 13), а при a < b он сжимается к оси ординат.
, нанесем соответствующие точки (x; y) на график и соединим их плавной линией. Аналогично рассуждая, достроим эллипс. При a > b эллипс сжимается к оси абсцисс (рис. 13), а при a < b он сжимается к оси ординат.
 |

Рис. 13. Эллипс  где a > b
где a > b
Указание. При a = b получаем параметрические уравнения окружности с центром в начале координат и радиусом а: 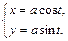
***
Настройка окон программы MathCAD для построения линий в полярной и декартовой системах координат:
· На главной панели инструментов Math нажмите на кнопки  ,
,  и
и  (если главной панели инструментов на экране нет, то V iew ® Toolbars ® M ath). Первая кнопка открывает панель Calculator, вторая – панель Graph, а третья – панель Greek Symbol.
(если главной панели инструментов на экране нет, то V iew ® Toolbars ® M ath). Первая кнопка открывает панель Calculator, вторая – панель Graph, а третья – панель Greek Symbol.
Для построения линий в полярной и декартовой системах координат:
· Введите уравнения линий, используя, если нужно, панель Calculator. Образец для линии в полярной системе координат: r(j):=5×cos(j), где j находится на панели Greek Symbol. Образец для линии, заданной параметрически: 
 . Знак присваивания «:=» вводится с клавиатуры нажатием комбинации клавиш Shift+«:».
. Знак присваивания «:=» вводится с клавиатуры нажатием комбинации клавиш Shift+«:».
· Нажмите на нужную кнопку  или
или  на панели Graph, первая из которых используется для построения линий в полярной системе координат, а вторая – для построения линий, заданных параметрически, в декартовой прямоугольной системе координат.
на панели Graph, первая из которых используется для построения линий в полярной системе координат, а вторая – для построения линий, заданных параметрически, в декартовой прямоугольной системе координат.
· В появившемся шаблоне заполните все поля как показано на примере.


· Щелкните на свободном поле.
· При необходимости увеличьте размер рисунка, потянув мышкой за правый нижний уголок рамки.
· Для получения на рисунке координатных осей двойным щелчком мыши по графику вызовите окно параметров Formatting Currently Selected Polar Plot и на вкладке Polar Axes / X-Y Axes выберите стиль осей Crossed ® OK.
Таблица 1
| № вар. | Задание | № вар. | Задание |
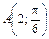 , , 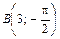 , ,  |  , ,  , , 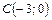 | ||
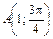 , ,  , ,  | 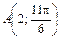 , ,  , ,  | ||
 , ,  , ,  |  , ,  , ,  |
Продолжение табл. 1
| № вар. | Задание | № вар. | Задание |
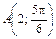 , ,  , , 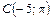 |  , ,  , , 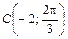 | ||
 , ,  , ,  |  , , 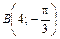 , , 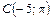 | ||
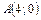 , ,  , ,  |  , , 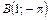 , ,  | ||
 , ,  , ,  |  , ,  , ,  | ||
 , ,  , , 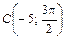 | 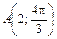 , ,  , ,  | ||
 , ,  , ,  |  , ,  , ,  | ||
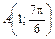 , ,  , ,  | 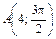 , ,  , ,  | ||
 , ,  , ,  |  , ,  , ,  | ||
 , ,  , , 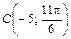 |  , ,  , ,  | ||
 , ,  , ,  |  , ,  , ,  |
Таблица 2
| № вар. | А) | Б) | В) |
 |  |  | |
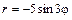 |  |  | |
 |  |  | |
 |  |  | |
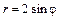 |  | 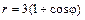 | |
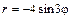 | 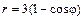 |  | |
 | 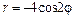 |  | |
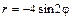 |  |  | |
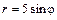 |  |  |
Продолжение табл. 2
| № вар. | А) | Б) | В) |
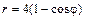 |  | 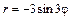 | |
 |  | 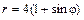 | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 | 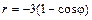 |  | |
 | 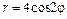 |  | |
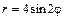 |  | 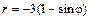 | |
 |  |  | |
 | 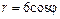 |  | |
 |  |  | |
 | 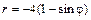 |  | |
 |  |  | |
 |  |  |
Таблица 3
| № вар. | А) | Б) |
 | 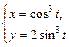 | |
 |  | |
 | 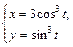 | |
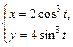 |  | |
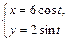 |  |
Продолжение табл. 3
| № вар. | А) | Б) |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
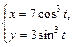 |  | |
 |  | |
 |  | |
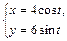 |  | |
 |  | |
 | 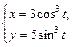 | |
 |  |
Окончание табл. 3
| № вар. | А) | Б) |
 |  | |
 |  | |
 | 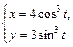 | |
 | 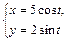 | |
 | 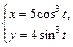 | |
 | 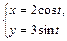 | |
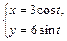 | 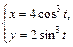 | |
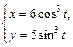 |  |
 2015-10-22
2015-10-22 9521
9521








