Геометрический смысл определенного интеграла

Если 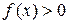на отрезке , то определенный интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции , прямым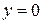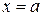и: , и .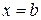

Если меняет знак на отрезке , то дает алгебраическую сумму площадей фигур, ограниченных линиями , , 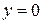, 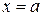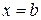. Причем площади, расположенные выше оси , входят в эту сумму со знаком плюс, а площади, расположенные ниже оси , – со знаком минус.

Методы вычислений