2015-10-22
305
Если 
– некоторая первообразная для функции 
, то определенный интеграл может быть вычислен по формуле Ньютона-Лейбница:
.
Эта формула устанавливает связь между неопределенным и определенным интегралами.
Примеры. Вычислить интегралы.
1. 
Замена переменных в определенном интеграле
Если функция 
непрерывна на отрезке 
, а функция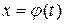 
дифференцируема на отрезке 
, причем 
, 
, то
Обратите внимание, при замене переменной в определенном интеграле меняют пределы интегрирования, а к старым переменным не возвращаются.
Примеры. Вычислить интегралы.
1. 
.
2. 
.
3. 
