Примеры решения задач

Задача 1. Выпишите первые шесть членов последовательности , заданной формулой п -го члена: .

Решение: Для нахождения любого члена последовательности необходимо вместо индекса п подставить его номер (в нашем случае – числа 1, 2, 3, 4, 5 и 6) и выполнить необходимые вычисления. Получим: а ₁ = 1³ – 2¹ + 1 = 0; а ₂ = 2³ – 2² + 1 = 5; а ₃ = 3³ – 2³ + 1 = 20; а ₄ = 4³ – 2⁴ + 1 = 49; а ₅ = 5³ – 2⁵ + 1 = 94; а ₆ = 6³ – 2⁶ + 1 = 153.

Задача 2. Выпишите первые семь членов последовательности , если , и для всех п выполняется равенство: .

Решение: Данная последовательность задана рекуррентным соотношением. Члены а_п, а_{п+ 1}, а_{п +2} – последовательные. 1) а_п = а ₁ = 2,

а_{п+ 1} = а ₂ = 3, тогда а_{п +2} = а ₃ = 3·2 − 2·3 = 0. 2) Теперь а_п = а ₂ = 3, а_{п+ 1} = а ₃ = 0; значит, а_{п +2} = а ₄ = 3·3 – 2·0 = 9. 3) а ₅ = 3·0 – 2·9 = −18;

а ₆ = 3·9 – 2·(−18) = 27 + 36 = 63; а ₇ = 3·(−18) – 2·63 = −54 – 126 = −180.

Задача 3. Найдите первый отрицательный член арифметической прогрессии: 12,5; 11,2; ….

Решение: 1 способ. Найдем разность заданной прогрессии, пользуясь формулой: .

d = 11,2 – 12,5 = −1,3. Теперь воспользуемся формулой, вытекающей из определения арифметической прогрессии:

а_{п +1} = а_п + d, и будем выписывать все последующие члены до тех пор, пока не дойдем до первого отрицательного:

а ₃ = 11,2 + (−1,3) = 11,2 – 1,3 = 9,9;

а ₄ = 9,9 – 1,3 = 8,6; а ₅ = 8,6 – 1,3 = 7,3 и т.д. Получим:

12,5; 11,2; 9,9; 8,6;..; 7,3; 6; 4,7; 3,4; 2,1; 0,8; −0,5; ….Нетрудно подсчитать, что первый отрицательный член стоит на одиннадцатом месте.

Замечание. Данный способ решения уместен, если нужный член находится достаточно быстро, а производимые вычисления не громоздки. В остальных случаях используют алгебраический способ с применением формулы п -го члена.

2 способ. d = 11,2 – 12,5 = −1,3. Обозначим искомый член последовательности а_п (так как мы не знаем его номера) и воспользуемся формулой п -го члена арифметической прогрессии: . а_п = 12,5 + (п – 1)·(−1,3). Так как а_п по условию отрицателен, необходимо решить линейное неравенство

12,5 + (п – 1)·(−1,3) < 0 относительно переменной п.

12,5 – 1,3 п + 1,3 <0; 12,5 +1,3 < 1,3 п; 1,3 п > 13,8; п > 13,8: 1,3; п > 10,6….

Таким образом, первое натуральное число, следующее за числом 10,6…, – 11. Значит, первый отрицательный член данной арифметической прогрессии стоит на одиннадцатом месте. Найдем его:

а ₁₁ = а ₁ + 10 d; а ₁₁ = 12,5 + 10·(−1,3) = 12,5 – 13 = −0,5.

Задача 4. Найдите сумму всех натуральных чисел от 1 до 200 включительно.

Решение: Последовательность натуральных чисел является арифметической прогрессией, у которой а ₁ = 1, d = 1. Воспользуемся формулой: . Для нашей задачи п = 200, а_п = а ₂₀₀, поэтому она будет выглядеть так: или . Подставляя известные данные, получим:
S ₂₀₀ = (1+200) ·100 = 201·100 = 20100.

Тема 2. Предел функции.

Задача 5. Вычислите предел функции:

Решение: При непосредственной подстановке числа 1 вместо переменной х получаем неопределенное выражение вида 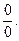В этом случае необходимо сократить дробь на множитель, стремящийся к нулю. Для этого в числителе вынесем за скобки общий множитель х, а знаменатель представим в виде произведения по формуле разложения на множители квадратного трехчлена. Получим: .

Задача 6. Вычислите предел функции: .

Решение: При непосредственной подстановке нуля вместо переменной х мы снова получим неопределенность вида 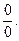В этом случае необходимо домножить числитель и знаменатель дроби на выражение, сопряженное числителю, т.е. на сумму . Получим: .

Задача 7. Вычислите предел: .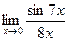

Решение: И в этом случае после подстановки получаем неопределенность вида 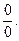Используя первый замечательный предел, а также тот факт, что функции sin 7 x и 7 х являются эквивалентными бесконечно малыми величинами при х →0, запишем: .

Задача 8. Вычислите предел: .

Решение: А здесь получается другая неопределенность − . По правилу раскрытия неопределенности данного вида необходимо разделить числитель и знаменатель дроби на переменную в наибольшей из имеющихся степеней, в нашем случае – на х ³. Выполняем преобразования: = .

Тема 3. Производная и дифференциал.

Задача 9. Продифференцируйте функцию .

Решение: Данная функция является сложной вида , где . Согласно правилу дифференцирования сложной функции, находим: .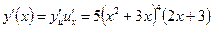

Задача 10. Вычислите приближенно .

Решение: Воспользуемся формулой для приближенных вычислений: 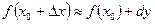. Так как 46 = 45 + 1, то в нашем примере

х ₀ = 45, ∆ х = 1; tg 45° = 1. Чтобы воспользоваться приведенной выше формулой, угол нужно выразить в радианах: х =π/4 и dx = ∆ х = 0,0175. Вычисляем дифференциал функции при заданных значениях:

. Следовательно, ∆ у ≈ 0,0350. Теперь находим:

. Вычисления с помощью четырехзначных таблиц дают: tg 46° = 1,0355.

Задача 11. Вычислите приближенно .

Решение: В данном случае можно воспользоваться специальной упрощенной формулой, выведенной из общей: .

Вычисляем: .

Задача 12. Вычислите приближенно 2,005⁴.

Решение: Для такого рода приближенных вычислений существует другая упрощенная формула, также выведенная из общей:

. Воспользуемся ею:

Тема 4. Применения производной.

Задача 13. Найдите угол наклона касательной к кривой у = 2 х ³ + 4 в точке (1; 6).

Решение: Исходя из геометрического смысла производной, угловой коэффициент касательной (или тангенс угла ее наклона к положительному направлению оси Ох) – это производная функции в точке касания. Получаем: . Таким образом, tg α = 6. Угол наклона находим в четырехзначных таблицах Брадиса: α ≈ 80° 32′.

Задача 14. Напишите уравнение касательной, проведенной к графику функции у = х ² – 3 х в точке с абсциссой х ₀ = 2.

Решение: Уравнение касательной имеет вид:

у = f (x ₀) + f ′(x ₀)(x – x ₀).

1) f (x ₀) = 2² − 3·2 = −2; 2) f ′(x) = 2 x – 3;

3) f ′(x ₀) = f ′(2) = 1.

Уравнение касательной: у = −2 + 1·(х – 2); у = х – 4.

Задача 15. Исследуйте функцию f (x) = x ³ – 3 x ² на возрастание, убывание и экстремумы.

Решение: , т.к. f – многочлен. Найдем производную функции: f ′(x) = 3 х ² – 6 х. Найдем критические точки функции (по определению, критическими точками функции называются внутренние точки области ее определения, в которых производная равна нулю или не существует). Точек, в которых производная не существует, нет, поэтому вычислим те, в которых она равна нулю. Решаем уравнение:

3 х ² – 6 х = 0; 3 х (х – 2) = 0; отсюда х = 0 или х = 2.

	f

Определим знаки производной на полученных интервалах.

(−∞; 0]: f′ (−1) = 3(−1)² – 6(−1) = 3 + 6 = 9; 9 > 0;

[0; 2]: f′ (1) = 3·1² − 6·1 = − 3; − 3 < 0;

[2; +∞): f′ (3) = 3·3² − 6·3 = 27 – 18 = 9; 9 > 0.

Функция возрастает на интервалах (−∞; 0] и

[2; +∞); убывает на интервале [0; 2].

Точки экстремумов: х_max = 0, x_min = 2.

Экстремумы: f_max = f (0) = 0³ − 3·0² = 0,

f_min = f (2) = 2³ − 3·2² = −4.

Задача 16. Исследуйте кривую у = х ³ – 6 х ² + 4 на выпуклость, вогнутость и точки перегиба.

−

Решение: D (y) = R, т.к. у – многочлен. Для выполнения задания необходимо найти вторую производную функции и использовать правило дождя: .

у′ = 3 х ² – 12 х; у" = 6 х – 12.

Из уравнения 6 х – 12 = 0 находим х = 2.

Вывод: на интервале (−∞; 2] график функции выпуклый, а на интервале [2; +∞) – вогнутый; в точке х = 2 – перегиб.

Задача 17. Точка движется прямолинейно по закону S (t) = 2 t ³ + t ² – 4. Найдите ее скорость и ускорение в момент времени t = 3.

Решение: Из механического смысла производной следует, что скорость точки – это производная от ее перемещения, а ускорение – производная от скорости или вторая производная от перемещения, т.е.

v (t) = S ′(t), a (t) = v ′(t) = S" (t). Находим: v (t) = (2 t ³ + t ² – 4)′ = 6 t ²+ 2 t,

v (3) = 6·3² + 2·3 = 60, a (t) = (6 t ²+ 2 t)′ = 12 t + 2; a (3) = 12·3 + 2 = 38.

Тема 5. Неопределенный интеграл.

Задача 18. Вычислите неопределенный интеграл: .

Решение: Произведем почленное деление и используем таблицу простейших интегралов.

=

=

Задача 19. Вычислите неопределенный интеграл .

Решение: Применим способ подстановки.

Задача 20. Вычислите неопределенный интеграл, используя способ интегрирования по частям: .

Решение: Формула интегрирования по частям: .

Пусть и = х, dv = e^xdx, тогда du = dx, v = e^x. Вычисляем:

Тема 6. Определенный интеграл и его приложения

Задача 21. Вычислите площадь фигуры, ограниченной линиями ху = 6 и х + у – 7 = 0.

Решение: Изобразим фигуру, площадь которой нужно найти.

Найдем абсциссы точек пересечения равносторонней гиперболы и прямой, для чего решим систему уравнений:

Имеем: х (7 – х) = 6; 7 х – х ² = 6; х ² – 7 х + 6 = 0, откуда х ₁ = 6, х ₂ = 1. Таким образом, a = 1, b = 6. Теперь применим формулу:

. В нашем случае .

=

= .

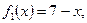
Тема 7. Простейшие дифференциальные уравнения

Задача 22. Решите дифференциальное уравнение:

Решение: Это уравнение с разделенными переменными, так как соответствует его общему виду

Интегрируя данное уравнение, получаем: , откуда или . Выразив у из уравнения, получим окончательный ответ: 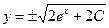. Заметим, что ответ можно было оставить в виде:

Задача 23. Найти все решения дифференциального уравнения .

Решение: Очевидно, что у = 0 не является решением данного уравнения, поэтому мы можем разделить обе его части на у ². Получаем: 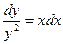и, следовательно, после интегрирования . Выражая их данного равенства у, получаем окончательный ответ (общее решение данного уравнения): , где С – произвольная постоянная.

Тема 8. Элементы линейной алгебры

Задача 24. Найти линейную комбинацию матриц .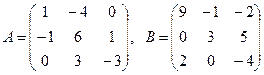

Решение:

1)

2) Чтобы умножить матрицу на некоторое число, нужно умножить на это число каждый элемент матрицы. Выполняем умножение:

.

3) Чтобы сложить две матрицы, необходимо сложить их соответствующие элементы. Получаем:

.

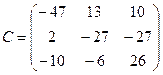Это и есть матрица, являющаяся линейной комбинацией исходных матриц.

Задача 25. Выполнить умножение матриц

и .

Решение: На умножении матриц остановимся подробнее.

Пусть даны матрицы

А = и В = .

Матрица С = называется произведением матриц А и В, если ее элементы находятся по следующему правилу:

Первая строка:

1. (каждый элемент первой строки матрицы А умножается на соответствующий элемент первого столбца матрицы В и полученные произведения складываются);
2. (каждый элемент первой строки матрицы А умножается на соответствующий элемент второго столбца матрицы В и полученные произведения складываются);
3. (каждый элемент первой строки матрицы А умножается на соответствующий элемент третьего столбца матрицы В и полученные произведения складываются);
4. И так далее (первая строка матрицы А умножается последовательно на столбцы матрицы В), пока не закончатся столбцы.

Вторая строка:

1. (каждый элемент второй строки матрицы А умножается на соответствующий элемент первого столбца матрицы В и полученные произведения складываются);
2. (каждый элемент второй строки матрицы А умножается на соответствующий элемент второго столбца матрицы В и полученные произведения складываются);
3. (каждый элемент второй строки матрицы А умножается на соответствующий элемент третьего столбца матрицы В и полученные произведения складываются);
4. И так далее (вторая строка матрицы А умножается последовательно на столбцы матрицы В), пока не закончатся столбцы.

Третья строка (и все последующие) находятся аналогично.

Вывод: Умножаемые матрицы могут быть разного размера, важно только, чтобы количество столбцов первой матрицы было равно количеству строк второй матрицы: .

А теперь выполним умножение заданных матриц:

Попробуйте выполнить еще одно умножение и проверьте себя:

.