2015-10-22
982
Относительно аффинной системы координат в пространстве 
две плоскости заданы своими уравнениями:
.
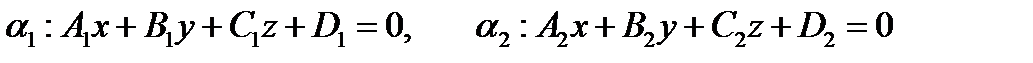Пусть в уравнении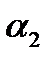 
: 
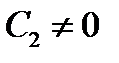. Тогда определяются точка 
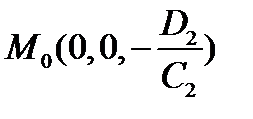, принадлежащая плоскости, и два вектора 
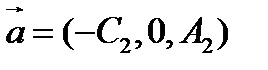и 
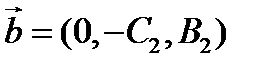, параллельные этой плоскости.
Плоскост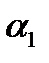и 
и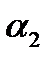 
совпадают тогда и только тогда, когда векторы 
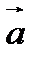и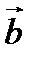 
параллельны плоскости 
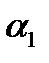и точка 
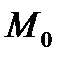принадлежит этой плоскости:
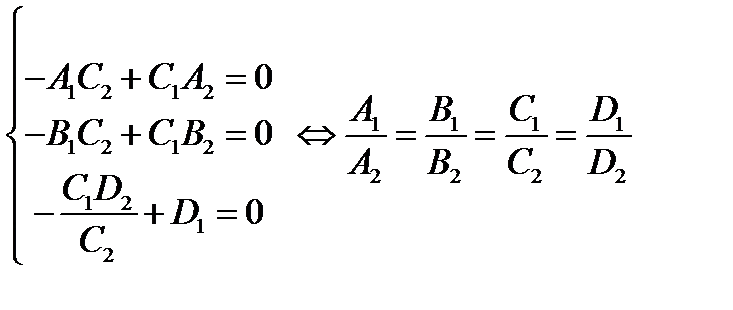– коэффициенты и свободные члены в общих уравнениях плоскостей пропорциональны.
Плоскост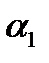и и 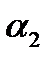параллельны тогда и только тогда, когда векторы 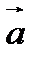и 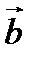параллельны плоскости 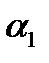и точка 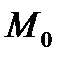не принадлежит этой плоскости:
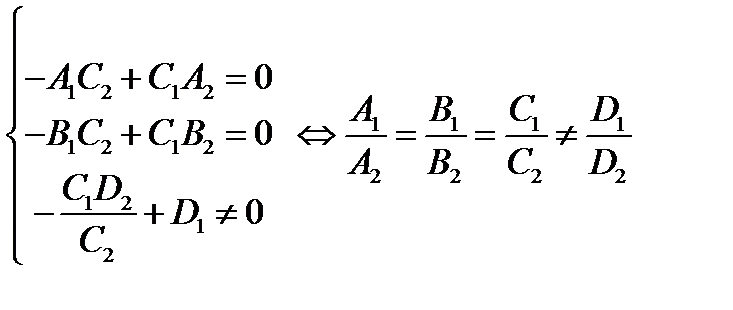– в общих уравнениях плоскостей коэффициенты пропорциональны и не пропорциональны свободным членам.
Плоскост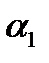и и 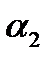пересекаются тогда и только тогда, когда хотя бы один из векторов 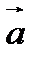и 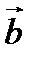не параллелен плоскости 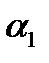, то есть имеет место хотя бы одно из неравенств 
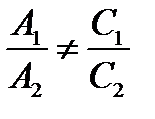или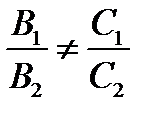 
, а значит, в общих уравнениях плоскостей коэффициенты не пропорциональны.
