О п р е д е л е н и е. Аффинной системой координат в пространстве (аффинным репером) называется точка и три некомпланарных вектора:  .
.
Прямые  ,
, 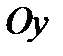 ,
, 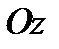 , определяемые точкой
, определяемые точкой  и векторами
и векторами 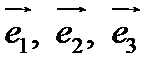 называются соответственно осью абсцисс, осью ординат и осью аппликат.
называются соответственно осью абсцисс, осью ординат и осью аппликат.
Частным случаем аффинной системы координат является прямоугольная система координат  , определяемая точкой
, определяемая точкой  и ортогональными ортами
и ортогональными ортами  .
.
О п р е д е л е н и е. Вектор  называется радиус-вектором точки
называется радиус-вектором точки  .
.
О п р е д е л е н и е. Координатами точки называются координаты её радиус-вектора:
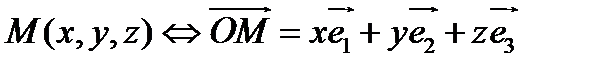 .
.
У п р а ж н е н и е. Построить точку по координатам в заданном аффинном репере в пространстве.
Аналогично тому, как это делалось на плоскости, с помощью координат решаются простейшие задачи
- Определение координат вектора по координатам начала и конца в аффинной системе координат.
- Определение координат точки по заданному простому отношению трех точек прямой и координатам двух из них в аффинной системе координат.
- Вычисление расстояния между точками по координатам относительно прямоугольной системы координат
 .
.
Задавая в пространстве аффинную систему координат, мы устанавливаем взаимно однозначное соответствие между точками и упорядоченными тройками действительных чисел. Это позволяет находить условие, определяющее геометрическую фигуру.
Под условием, определяющим геометрическую фигуру, понимаем упорядоченные тройки действительных чисел, уравнения, неравенства или их системы, которым удовлетворяют координаты любой точки, принадлежащей фигуре, и не удовлетворяют координаты точек, не принадлежащих фигуре.
Тогда геометрическую задачу можно перевести на язык алгебры, решить методами алгебры и полученный результат интерпретировать геометрически.
Через данную точку  проходит единственная плоскость
проходит единственная плоскость 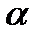 , параллельная двум данным неколлинеарным векторам
, параллельная двум данным неколлинеарным векторам 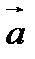 и
и 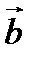 .
.
Пусть в пространстве задан аффинный репер  и
и  ,
,  . Точка
. Точка  принадлежит плоскости
принадлежит плоскости 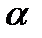 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 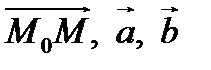 компланарны, то есть вектор
компланарны, то есть вектор 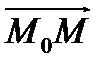 можно выразить через векторы
можно выразить через векторы  и
и 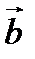 :
:
 .
.
Переходя к координатам, найдем уравнения, которым должны удовлетворять координаты 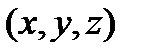 точки, принадлежащей плоскости:
точки, принадлежащей плоскости:
 – параметрические уравнения плоскости.
– параметрические уравнения плоскости.
Условием компланарности векторов 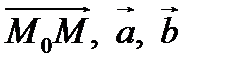 является равенство нулю определителя, составленного из координат этих векторов:
является равенство нулю определителя, составленного из координат этих векторов:
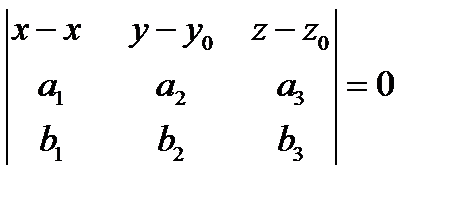 – общее уравнение плоскости.
– общее уравнение плоскости.
Общее уравнение плоскости приводится к виду
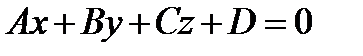 , где
, где 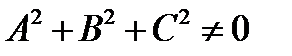 .
.
Пусть плоскость  пересекает все три оси координат в точках
пересекает все три оси координат в точках 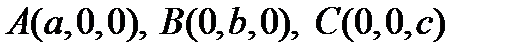 . Имеем два неколлинеарных вектора
. Имеем два неколлинеарных вектора  и
и 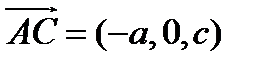 , параллельных плоскости
, параллельных плоскости  . Тогда получаем уравнение плоскости
. Тогда получаем уравнение плоскости
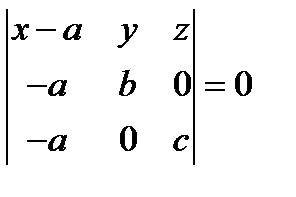 или
или  – уравнение плоскости в отрезках.
– уравнение плоскости в отрезках.
Через данную точку  проходит единственная плоскость
проходит единственная плоскость 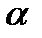 , перпендикулярная данному ненулевому вектору
, перпендикулярная данному ненулевому вектору 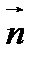 . Вектор
. Вектор 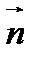 , как и любой другой ненулевой вектор, перпендикулярный плоскости
, как и любой другой ненулевой вектор, перпендикулярный плоскости 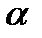 , называется нормальным вектором плоскости.
, называется нормальным вектором плоскости.
Точка  принадлежит плоскости
принадлежит плоскости 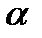 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 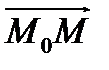 и
и 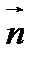 ортогональны, то есть их скалярное произведение равно нулю. Чтобы выразить условие ортогональности векторов через координаты, необходим ортонормированный базис, а значит, в пространстве должна быть задана прямоугольная система координат
ортогональны, то есть их скалярное произведение равно нулю. Чтобы выразить условие ортогональности векторов через координаты, необходим ортонормированный базис, а значит, в пространстве должна быть задана прямоугольная система координат 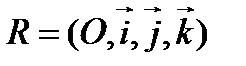 . Пусть
. Пусть 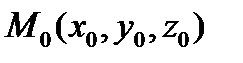 ,
,  . Выразив условие ортогональности векторов
. Выразив условие ортогональности векторов 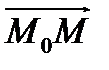 и
и  через координаты, получим уравнение плоскости
через координаты, получим уравнение плоскости 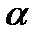 :
:  .
.
Выводы:
1. Чтобы составить уравнение плоскости, надо знать точку и два неколлинеарных вектора, параллельных этой плоскости, либо точку и нормальный вектор.
2. Уравнение плоскости приводится к виду
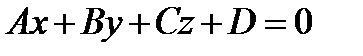 , где
, где 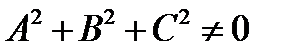 ,
,
то есть плоскость является алгебраической поверхностью первого порядка.
Т е о р е м а. Любая алгебраическая поверхность первого порядка является плоскостью.
Д о к а з а т е л ь с т в о. Для алгебраической поверхности первого порядка существует аффинная система координат, относительно которой поверхность задается уравнением 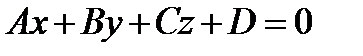 , где
, где 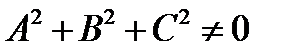 .
.
Пусть  . Приведя уравнение поверхности к виду
. Приведя уравнение поверхности к виду  , получим равносильное уравнение
, получим равносильное уравнение
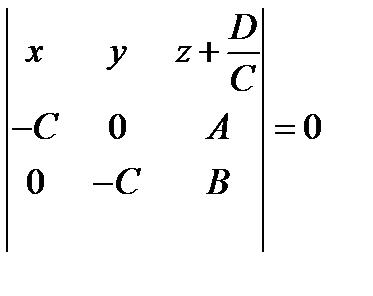 .
.
Это есть уравнение плоскости, проходящей через точку  параллельно векторам
параллельно векторам  и
и  .
.
 2015-10-22
2015-10-22 6675
6675
