Условие параллельности плоскости и вектора

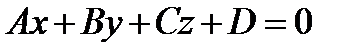Относительно аффинной системы координат плоскость задана уравнением . Найдем условие параллельности вектора 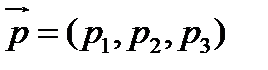плоскости .

От точки , принадлежащей плоскости 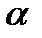, отложим вектор . Точка будет иметь координаты

.

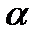Вектор параллелен плоскости тогда и только тогда, когда точка лежит в плоскости , то есть

.

Подставляя координаты точки и учитывая, что , получим условие параллельности вектора и плоскости:

. (*)

Очевидно, вектор не параллелен плоскости . Если система координат прямоугольная, то из условия (*) следует, что вектор ортогонален любому вектору 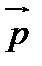, параллельному плоскости, то есть является нормальным вектором этой плоскости.