Относительно аффинной системы координат в пространстве  плоскость
плоскость  задана уравнением
задана уравнением 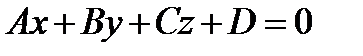 .
.
Выражение  называется четырехчленом плоскости.
называется четырехчленом плоскости.
От точки  отложим вектор
отложим вектор 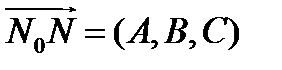 . Так как этот вектор не параллелен плоскости, то точка
. Так как этот вектор не параллелен плоскости, то точка  не лежит в этой плоскости.
не лежит в этой плоскости.
Для произвольной точки 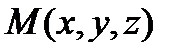 пространства существует точка
пространства существует точка 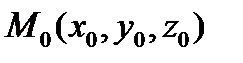 в плоскости
в плоскости  , такая, что
, такая, что 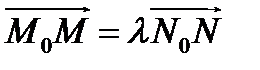 . При этом,
. При этом,  , если точки
, если точки  и
и  лежат по одну сторону от
лежат по одну сторону от  , и
, и  , если точки
, если точки  и
и  лежат по разные стороны от
лежат по разные стороны от  . Находим координаты точки
. Находим координаты точки 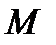
 .
.
Находим значение четырехчлена плоскости от координат точки 
 .
.
Таким образом, для всех точек пространства, лежащих с точкой  по одну сторону от
по одну сторону от  , значение четырехчлена плоскости больше нуля, а для всех точек пространства, лежащих с
, значение четырехчлена плоскости больше нуля, а для всех точек пространства, лежащих с  по разные стороны от
по разные стороны от  , значение четырехчлена плоскости меньше нуля. Имеем геометрический смысл знака четырехчлена:
, значение четырехчлена плоскости меньше нуля. Имеем геометрический смысл знака четырехчлена:
каждое из неравенств
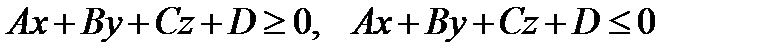
определяет полупространство, границей которого является плоскость, задаваемая уравнением  .
.
 2015-10-22
2015-10-22 844
844








