2015-10-22
4165
1. Умножение матрицы на число. Чтобы умножить матрицу на число, нужно все элементы матрицы умножить на это число.
2. Сложение и вычитание матриц. Эти операции определяются только для матриц одинаковой размерности.
Суммой (разностью) матриц 
и 
, обозначаемой 
(
) называется матрица 
, элементы которой 
(
).
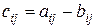Например. Найти линейную операцию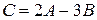 
,
если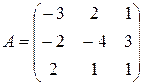 
, 
.
Итак, согласно первому и второму пунктам:
3. Умножение матриц. Эта операция не относиться к линейной.
Произведением матриц 
и 
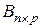называется матрица 
(проще записывается 
), элементы которой
,
где 
, 
- элементы матриц и - соответственно.
Отсюда следует, что произведение 
существует только в случае, когда первый множитель имеет число столбцов равное числу строк второго множителя .
Далее, число строк матрицы 
равно числу строк , а число столбцов – числу столбцов .
Из существования произведения 
не следует существования произведения 
. Как правило, 
. Если 
, то матрицы и называются перестановочными (или коммутирующими). Известно, что всегда 
.
Например. Даны матрицы 
и 
. Найти и 
.
( выполняется, так как число столбцов равно числу строк )
( выполняется, так как число столбцов равно числу строк )
