Введем понятие ранга матрицы. Выделим в матрице 
 -строк и
-строк и  -столбцов, где
-столбцов, где  - число, меньшее или равное меньшему из чисел
- число, меньшее или равное меньшему из чисел 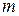 и
и 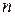 . Определитель порядка
. Определитель порядка  , составленный из элементов, стоящих из пересечения выделенных
, составленный из элементов, стоящих из пересечения выделенных  -строк и
-строк и  -столбцов, называется минором или определителем, порожденным матрицей
-столбцов, называется минором или определителем, порожденным матрицей  .
.
Рангом матрицы  (обозначается
(обозначается  ) называется наибольший порядок порожденных ею определителей, отличных от нуля.
) называется наибольший порядок порожденных ею определителей, отличных от нуля.
Ранг матрицы не изменится, если:
1) поменять местами любые два параллельных ряда;
2) умножить (разделить) каждый элемент ряда на один и тот же множитель (делитель)  ;
;
3) прибавить к элементам ряда соответствующие элементы любого другого параллельного ряда, умноженные на один и тот же множитель;
4) Ряд, состоящий из нулей, отбрасывается.
Преобразования 1-4 называются элементарными. Две матрицы называются эквивалентными, если одна матрица получается из другой с помощью элементарных преобразований. Эквивалентность матриц  и
и  обозначается
обозначается  ~
~  .
.
Базисным минором матрицы называется всякий отличный от нуля минор, порядок которого равен рангу данной матрицы.
Рассмотрим основные методы нахождения ранга матрицы.
1. Метод единиц и нулей. С помощью элементарных преобразований можно любую матрицу привести к виду, когда каждый ее ряд будет состоять только из нулей, или нулей и одной единицы. Тогда число оставшихся единиц и определит ранг исходной матрицы, так как полученная матрица будет эквивалентна исходной.
Пример 2.1. Найти ранг матрицы методом единиц и нулей.
 ~
~
1 шаг.
Разделим элементы третьего столбца на 2, затем первую строку умножим на  и сложим с четвертой строкой. Получим новую эквивалентную матрицу:
и сложим с четвертой строкой. Получим новую эквивалентную матрицу:
~  ~
~
2 шаг.
Теперь четвертую строчку складываем со второй и с третьей. Получим новую эквивалентную матрицу:


 ~
~  ~
~

 +
+


 +
+  +
+
3 шаг.
Умножим элементы второго столбца на  и сложим с элементами четвертого столбца. Затем умножим элементы второго столбца на
и сложим с элементами четвертого столбца. Затем умножим элементы второго столбца на  и сложим с соответствующими элементами первого столбца. И окончательно элементы второго столбца сложим с соответствующими элементами пятого столбца. Получим новую эквивалентную матрицу:
и сложим с соответствующими элементами первого столбца. И окончательно элементы второго столбца сложим с соответствующими элементами пятого столбца. Получим новую эквивалентную матрицу:

 ~
~  ~
~
4 шаг.
Умножим элементы третьей строки на  и сложим с соответствующими элементами второй строки. Получим новую эквивалентную матрицу:
и сложим с соответствующими элементами второй строки. Получим новую эквивалентную матрицу:

 ~
~  ~
~
+
 |
5 шаг.
Сложим элементы пятого столбца с соответствующими элементами первого столбца. Получим новую эквивалентную матрицу:
~  ~
~

 +
+ 
6 шаг.
Умножим элементы третьего столбца на 3 и сложим с соответствующими элементами первого столбца. Получим новую эквивалентную матрицу:

 ~
~  ~
~

 +
+  +
+
7 шаг.
Умножим на  элементы третьего столбца и сложим с соответствующими элементами второго и четвертого столбцов. Получим новую эквивалентную матрицу:
элементы третьего столбца и сложим с соответствующими элементами второго и четвертого столбцов. Получим новую эквивалентную матрицу:
 ~
~  ~
~

 +
+

8 шаг.
Умножим элементы четвертого столбца на  и сложим с соответствующими элементами пятого столбца. Затем просто умножим элементы четвертого столбца на
и сложим с соответствующими элементами пятого столбца. Затем просто умножим элементы четвертого столбца на  . Получим новую эквивалентную матрицу:
. Получим новую эквивалентную матрицу:
~  -
-  , так как осталось 3 единицы.
, так как осталось 3 единицы.
2. Метод окаймляющих миноров. Минор  порядка
порядка  , содержащий в себе минор
, содержащий в себе минор  порядка
порядка  , называется окаймляющим минором
, называется окаймляющим минором  . Если у матрицы
. Если у матрицы  существует минор
существует минор  , а все окаймляющие его миноры
, а все окаймляющие его миноры  , то
, то  .
.
Найдем этим методом  из предыдущего примера.
из предыдущего примера.

Начнем с левого верхнего угла:
 ;
;
 ;
;




Как видно, что эта матрица содержит всего два минора 4-го порядка. Проверим второй:




То есть 
ЗАДАНИЯ
Задание 2.1. Найти ранг матрицы
1) Методом единиц и нулей;
2) Методом окаймляющих миноров.
1.  ; ; | 2.  ; ; |
3.  ; ; | 4.  ; ; |
5.  ; ; | 6.  ; ; |
7.  ; ; | 8.  ; ; |
9.  ; ; | 10.  ; ; |
11.  ; ; | 12.  ; ; |
13.  ; ; | 14.  ; ; |
15.  ; ; | 16.  ; ; |
17.  ; ; | 18.  ; ; |
19.  ; ; | 20.  ; ; |
21.  ; ; | 22.  ; ; |
23.  ; ; | 24.  ; ; |
25.  ; ; | 26.  ; ; |
27.  ; ; | 28.  ; ; |
29.  ; ; | 30.  . . |
Обратная матрица
Квадратная матрица порядка 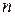
 называется невырожденной, если её определитель (детерминант)
называется невырожденной, если её определитель (детерминант)  .
.
В случае, когда  , матрица
, матрица  называется вырожденной.
называется вырожденной.
Только для квадратной невырожденной матрицы  вводится понятие обратной матрицы
вводится понятие обратной матрицы  .
.
Матрица  называется обратной для квадратной невырожденной матрицы
называется обратной для квадратной невырожденной матрицы  , если
, если  , где
, где 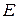 - единичная матрица порядка
- единичная матрица порядка 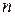 .
.
Для матрицы  существует единственная обратная матрица, которая определяется по формуле:
существует единственная обратная матрица, которая определяется по формуле:


 или
или  ,
,
где  или
или  - союзная или присоединённая матрица, её элементами являются алгебраические дополнения
- союзная или присоединённая матрица, её элементами являются алгебраические дополнения  транспонированной матрицы
транспонированной матрицы  , т.е. матрицы, полученной из данной матрицы
, т.е. матрицы, полученной из данной матрицы  заменой её строк столбцами с теми же номерами.
заменой её строк столбцами с теми же номерами.
 , т.е.
, т.е. 
Пример 2.2. Найти обратную матрицу двумя способами: с помощью алгебраических дополнений и путем элементарных преобразований. Сделать проверку.
Дана матрица  .
.
Найти:  .
.
Решение:
1 способ. С помощью алгебраических дополнений.
Найдем обратную матрицу по формуле  ,
,
где  - определитель матрицы
- определитель матрицы  ;
;
 - союзная или присоединённая матрица, состоящая из алгебраических дополнений транспонированной матрицы
- союзная или присоединённая матрица, состоящая из алгебраических дополнений транспонированной матрицы  .
.
Согласно формуле можно сказать, что если  , то обратная матрица не существует.
, то обратная матрица не существует.
Найдем:
 ,
,
значит обратная матрица существует.
Составим союзную матрицу, для этого найдем алгебраические дополнения по формуле

 ; ; |  ; ; |  ; ; |
 ; ; |  ; ; |  ; ; |
 ; ; |  ; ; |  . . |
Отсюда: 
 .
.
2 способ. Основан на элементарных преобразованиях вспомогательной матрицы, которая получается путём приписывания к данной матрице единичной матрицы того же порядка. Схематически это выглядит так:

Итак, запишем матрицу:




 ~
~  ~
~



 ~
~  ~
~  ~
~
~  ~
~



 ~
~  ~
~
~ 
Итак:

Проверка. Сделаем проверку исходя из свойства  . Остановимся на произведении
. Остановимся на произведении  . Для удобства умножения матриц
. Для удобства умножения матриц  запишем в виде:
запишем в виде:
 .
.
Тогда:



 - верно (смотри определение
- верно (смотри определение  )
)
Задание 2.2. Найти обратную матрицу двумя способами: с помощью алгебраических дополнений и путем элементарных преобразований. Сделать проверку.
1.  | 2.  |
3.  | 4.  |
5.  | 6.  |
7.  | 8.  |
9.  | 10.  |
11.  | 12.  |
13.  | 14.  |
15.  | 16.  |
17.  | 18.  |
19.  | 20.  |
21.  | 22.  |
23.  | 24.  |
25.  | 26.  |
27.  | 28.  |
29.  | 30.  |
III. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
 2015-10-22
2015-10-22 11396
11396
