Смешанное произведение векторов

В пространстве каждая тройка некомпланарных векторов, приложенных к одной точке, определяет некоторый параллелепипед, ребрами которого являются эти векторы. Объему этого параллелепипеда приписывается знак «+», если тройка векторов правая и «-», если левая. Такой параллелепипед называется ориентированным.

Смешанным (векторно-скалярным) произведением трех векторов называется число

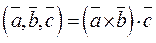
СВОЙСТВА:

1. Смешанное произведение равно объему ориентированного параллелепипеда, построенного на приведенных к общему началу некомпланарных векторах .

2. Смешанное произведение равно нулю, если векторы компланарны.

3.

4.

КООРДИНАТНАЯ ФОРМА СМЕШАННОГО ПРОИЗВЕДЕНИЯ.

Если вектор , то из определения смешанного произведения получим: