Полярная система координат

Рассмотрим радиус-вектор на плоскости:

Вектор определяется: - длиной ,

- углом относительно полярной оси .

Свяжем полярную систему координат с декартовой:

.

По теореме Пифагора:

Обратная связь:

или

или

ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ.

Цилиндрические координаты в пространстве обозначаются .

Координатными поверхностями в этой системе координат служат цилиндры , меридиональные полуплоскости (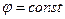), и плоскости, перпендикулярные оси

Через эти координаты декартовы переменные выражаются:

К цилиндрическим координатам удобно переходить, если заданная область имеет вид цилиндра или его части. При этом .