Задачу на построение точек пересечения прямой линии с кривой поверхностью решают аналогично решению первой основной позиционной задачи. Рассмотрим ее на конкретном примере, когда в качестве поверхности взята поверхность тора (рис. 67).
 Рис. 67
Рис. 67
| 1. Через данную прямую l проведем вспомогательную плоскость Г, которая в большинстве случаев берется проецирующей. Заключаем прямую l во фронтально – проецирующую плоскость Г (Г2), фронтальная проекция которой совпадает с l2, l2  Г2.
2. Построим линию пересечения данной поверхности и вспомогательной плоскости Г. Плоскость Г (Г2) пересекает поверхность по кривой Г2.
2. Построим линию пересечения данной поверхности и вспомогательной плоскости Г. Плоскость Г (Г2) пересекает поверхность по кривой 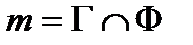 . Так как . Так как 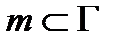 , то m2 = Г2. Горизонтальную проекцию m1 линии пересечения m строим по точкам из условия принадлежности их поверхности тора.
3. Находим точки пересечения I, || данной прямой l с построенной кривой m. , то m2 = Г2. Горизонтальную проекцию m1 линии пересечения m строим по точкам из условия принадлежности их поверхности тора.
3. Находим точки пересечения I, || данной прямой l с построенной кривой m.
|
4. Определим видимость. На горизонтальной проекции точки I1 и II1 – видимые, так как лежат на видимой части поверхности. На фронтальной проекции точка I2 – видимая, а точка II2 – невидимая.
Данное решение является типовым. Однако в каждом конкретном случае для упрощения построений целесообразно использовать другие виды вспомогательных плоскостей, а также преобразования комплексного чертежа.
 2015-10-22
2015-10-22 448
448








