Алгоритм решения систем линейных однородных уравнений

Находим ранг матрицы.
Выделяем базисный минор. Выделяем зависимые (базисные) и свободные неизвестные.
Вычеркиваем те уравнения системы, коэффициенты которых не вошли в состав базисного минора, так как они являются следствиями остальных (по теореме о базисном миноре).
Члены уравнений, содержащие свободные неизвестные, перенесем в правую часть. В результате получим систему из r уравнений с r неизвестными, эквивалентную данной, определитель которой отличен от нуля.
Решаем полученную систему методом исключения неизвестных. Находим соотношения, выражающие зависимые переменные через свободные.
Если ранг матрицы не равен количеству переменных, то находим фундаментальное решение системы.
В случае rang = n имеем тривиальное решение.

8. Определение 5.6. Если все свободные члены системы уравнений равны нулю, то такая система называется однородной, если же хотя бы один свободный член отличен от нуля, система называется неоднородной.

9. Теорема 5.1. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда определитель основной матрицы системы равен нулю.

10. Определение 5.7. Элементарными преобразованиями системы линейных уравнений называют следующие операции:

11. 1) сложение обеих частей одного уравнения с соответствующими частями другого, умноженных на одно и то же число, не равное нулю;

12. 2) перестановка уравнений местами;

13. 3) удаление из системы уравнений, являющихся тождествами.

14. Рассмотрим основные методы решения систем линейных уравнений.

Метод Гаусса

16.

17. Рассмотрим систему линейных уравнений Метод Гаусса решения систем линейных уравнений состоит из двух этапов, называемых прямым и обратным ходом. Прямой ход метода Гаусса заключается в том, что с помощью элементарных преобразований над расширенной матрицей система приводится к «ступенчатому» виду.

_18.Обратный ход метода Гаусса состоит в том, что, начиная с последнего уравнения ступенчатой системы, вычисляются неизвестные.

19. При реализации прямого хода метода Гаусса возможны следующие три случая.

20. 1. В результате преобразований в системе уравнений будет получено уравнение вида где Ясно, что никакой набор действительных чисел этому уравнению удовлетворять не может, поэтому в таком случае система уравнений несовместна.

21. 2. В результате преобразований получится ступенчатая система уравнений

22.

23. в которой количество уравнений совпадает с количеством неизвестных.

24. В этом случае система уравнений является определённой.

25. В результате преобразований получится система уравнений ступенчатого вида, в которой количество неизвестных больше числа уравнений системы ()

26.

27. В этом случае те неизвестные, которые стоят на «ступеньках», называются главными неизвестными (), а другие неизвестные называются свободными (); система уравнений будет неопределённой. Тогда обратный ход метода Гаусса состоит в том, что начиная с последнего уравнения системы, главные неизвестные выражаются через свободные и составляется общее решение системы уравнений. Для того чтобы получить какое-либо частное решение системы, свободным неизвестным придают конкретные числовые значения, вычисляя тем самым главные неизвестные.

28. Пример. Решить систему линейных уравнений методом Гаусса.

29.

30. Прямой ход. Приведём расширенную матрицу системы

31.

32. с помощью элементарных преобразований к ступенчатому виду. Переставим первую и вторую строки матрицы , получим матрицу

33.

34. Сложим вторую строку полученной матрицы с первой, умноженной на а её третью строку – с первой строкой, умноженной на Получим матрицу

35.

36. К третьей строке полученной матрицы прибавим вторую строку, умноженную на в результате чего получим ступенчатую матрицу

37.

38. Таким образом, мы привели данную систему уравнений к ступенчатому виду:

39. ,

40. Обратный ход. Начиная с последнего уравнения полученной ступенчатой системы уравнений, последовательно найдём значения неизвестных:

41. Однородная система линейных уравнений всегда совместна: она имеет хотя бы одно решение – нулевое (так называемое, тривиальное решение). Нас будут интересовать только нетривиальные решения однородной системы линейных уравнений. Рассмотрим пример решения однородной системы линейных уравнений методом Гаусса.

42. Пример. Решить систему линейных уравнений методом Гаусса.

43.

44. Прямой ход. Поскольку данная система уравнений является однородной, выясним, имеет ли эта система нетривиальные решения.
Для этого вычислим определитель основной матрицы системы

45.

46. Вычисляя определитель разложением по строке или по столбцу, получим В соответствии с теоремой 5.1, данная система линейных уравнений имеет нетривиальное решение. Приведём основную матрицу к ступенчатому виду с помощью элементарных преобразований. Сложим вторую и четвёртую строки матрицы с первой строкой, умноженной на а третью строку – с первой строкой, умноженной на получим матрицу

47.

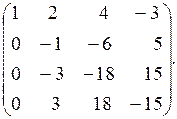
48. Сложим третью строку полученной матрицы со второй, умноженной на а четвёртую строку – с третьей строкой; получим матрицу

49.

50. В этой матрице удалим нулевые строки и получим ступенчатую матрицу

51.

52. Тем самым, данная система приведена к ступенчатому виду:

53.

54. Неизвестные и стоящие на «ступеньках», являются главными, а неизвестные и свободными.

55. Обратный ход. Выразим из второго уравнения системы главную неизвестную через свободные неизвестные и Используя полученное равенство, из первого уравнения ступенчатой системы получим следующее выражение главной неизвестной Общее решение данной системы уравнений запишем в виде: где и любые действительные числа. Положив, к примеру, и получим частное решение системы:

56.

57. 5.2. Матричный метод решения систем линейных уравнений

58.

59. Пусть дана система линейных уравнений с неизвестными:

60.

61. где

62.

63. Будем предполагать, что основная матрица невырожденная.
Тогда, по теореме 3.1, существует обратная матрица Помножив матричное уравнение на матрицу слева, воспользовавшись определением 3.2, а также утверждением 8) теоремы 1.1, получим формулу, на которой основан матричный метод решения систем линейных уравнений:

64.

65. Замечание. Отметим, что матричный метод решения систем линейных уравнений в отличие от метода Гаусса имеет ограниченное применение: этим методом могут быть решены только такие системы линейных уравнений, у которых, во-первых, число неизвестных равно числу уравнений, а во-вторых, основная матрица невырожденная.

66. Пример. Решить систему линейных уравнений матричным методом.

67.

68. Задана система трёх линейных уравнений с тремя неизвестными 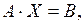где

69.

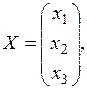
70. Основная матрица системы уравнений невырожденная, поскольку её определитель отличен от нуля:

71.

72. Обратную матрицу составим одним из методов, описанных в пункте 3.

73.

74. По формуле матричного метода решения систем линейных уравнений получим

75.

76.

Метод Крамера

78.

79. Данный метод так же, как и матричный, применим только для систем линейных уравнений, у которых число неизвестных совпадает с числом уравнений. Метод Крамера основан на одноимённой теореме:

80. Теорема 5.2. Система линейных уравнений с неизвестными

81.

82. основная матрица которой невырожденная, имеет единственное решение, которое может быть получено по формулам

83.

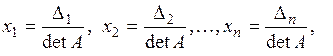
84. где определитель матрицы, полученной из основной матрицы системы уравнений заменой её 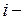го столбца столбцом свободных членов.

85. Пример. Найдём решение системы линейных уравнений, рассмотренной в предыдущем примере, методом Крамера. Основная матрица системы уравнений невырожденная, поскольку Вычислим определители