Примеры решения задач

Пример

Задание. Найти остаток от деления многочлена на двучлен

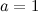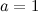Решение. Согласно теореме Безу искомый остаток равен значению многочлена в точке . Найдем тогда , для этого значение подставим в выражение для многочлена вместо . Будем иметь:

Ответ. Остаток равен 5Пример

Задание. С помощью теоремы Безу доказать, что многочлен делится на двучлен без остатка.

Решение. Указанный многочлен делится на заданный двучлен без остатка, если число - корень данного многочлена, то есть имеет место равенство: . Найдем значение многочлена в точке :

Что и требовалось доказать

Теорема Безу

Теорема. Остаток от деления многочлена на многочлен равен .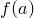

Доказательство. Степень остатка меньше 1, следовательно, остаток — константа. Пусть — остаток.

Это равенство верно при любых значениях . Положим :

Алгори́тм Евкли́да — эффективный алгоритм для нахождения наибольшего общего делителя двух целых чисел. Алгоритм назван в честь греческого математика Евклида, который впервые описал его в VII и X книгах «Начал».

В самом простом случае алгоритм Евклида применяется к паре положительных целых чисел и формирует новую пару, которая состоит из меньшего числа и разницы между большим и меньшим числом. Процесс повторяется, пока числа не станут равными. Найденное число и есть наибольший общий делитель исходной пары.

Теорема Виета