81. Задание {{ 103 }} ТЗ № 103
Отметьте правильный ответ
Матрицы, задающие одно и тоже линейное преобразование в разных базах …
£ совпадают
£ взаимно обратны
R подобны
£ единичны
82. Задание {{ 104 }} ТЗ № 104
Отметьте правильный ответ
Пусть 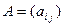 квадратная матрица порядка n. Тогда матрица
квадратная матрица порядка n. Тогда матрица 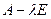 , где E - единичная матрица порядка n, называется …
, где E - единичная матрица порядка n, называется …
£ единичной матрицей
R характеристической матрицей А
£  - матрицей матрицы А
- матрицей матрицы А
£ диагональной матрицей
83. Задание {{ 105 }} ТЗ № 105
Отметьте правильный ответ
Пусть  – линейное преобразование
– линейное преобразование  и пусть для
и пусть для 
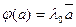 , где
, где  - некоторое действительное число, то вектор
- некоторое действительное число, то вектор 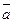 называется … преобразования
называется … преобразования 
£ единичным вектором
£ пропорциональным вектором
£ несобственным вектором собственным вектором
R собственным вектором
84. Задание {{ 106 }} ТЗ № 106
Отметьте правильный ответ
Пусть  – линейное преобразование
– линейное преобразование  и пусть для
и пусть для 
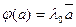 , где
, где  -…
-…
R собственное значение преобразования 
£ коэффициент преобразования 
£ постоянное преобразования 
£ число отличное от единицы
85. Задание {{ 107 }} ТЗ № 107
Отметьте правильный ответ
Линейное преобразование  тогда и только тогда задается в базисе
тогда и только тогда задается в базисе 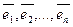 диагональной матрицей, если …
диагональной матрицей, если …
£ в базисе есть собственный вектор
R базис ортогональный
£  - тождественное
- тождественное
£ базис ортонормированный
86. Задание {{ 108 }} ТЗ № 108
Отметьте правильный ответ
Если 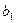 и
и  собственные векторы линейного преобразования
собственные векторы линейного преобразования  , относящиеся к различным значениям
, относящиеся к различным значениям 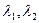 , то
, то 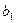 и
и  …
…
£ линейно зависимы
£ ортогональны
£ пропорциональны
R линейно независимы
87. Задание {{ 109 }} ТЗ № 109
Отметьте правильный ответ
Найти собственные значения линейного преобразования  заданного в некотором базисе матрицей
заданного в некотором базисе матрицей 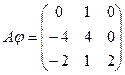
£ 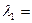 1,
1,  2,
2, 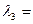 3
3
£ 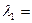

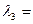 1
1
R 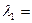

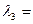 2
2
£ 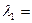

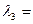 -3
-3
88. Задание {{ 110 }} ТЗ № 110
Отметьте правильный ответ
Линейное преобразование  задано матрицей
задано матрицей 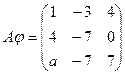 . При каком значении
. При каком значении 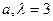 является собственным значением
является собственным значением 
R 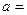 6
6
£ 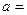 1
1
£ 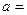 2
2
£ 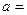 -6
-6
89. Задание {{ 111 }} ТЗ № 111
Отметьте правильный ответ
Найти собственные вектора линейного преобразования  заданного матрицей
заданного матрицей 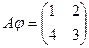 .
.
£  (-1,2),
(-1,2), 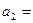 (2,3)
(2,3)
R  (-1,1),
(-1,1), 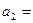 (2,1)
(2,1)
£  (1,-1),
(1,-1), 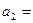 (1,3)
(1,3)
£  (-1,2),
(-1,2), 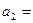 (2,3)
(2,3)
90. Задание {{ 112 }} ТЗ № 112
Отметьте правильный ответ
При каком значении  вектор x=(1,1,1) является собственным вектором линейного преобразования
вектор x=(1,1,1) является собственным вектором линейного преобразования  , заданного матрицей
, заданного матрицей 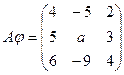
£  =7
=7
£  =-6
=-6
R  =-7
=-7
£  =6
=6
91. Задание {{ 113 }} ТЗ № 113
Отметьте правильный ответ
Линейное преобразование  задано матрицей
задано матрицей  и вектор x=(1,2,1) является собственным вектором
и вектор x=(1,2,1) является собственным вектором  . Найти собственное значение
. Найти собственное значение  для х и значение
для х и значение 
R  =-4,
=-4,  =1
=1
£  =1,
=1,  =2
=2
£  =2,
=2,  =1
=1
£  =4,
=4,  =-1
=-1
92. Задание {{ 114 }} ТЗ № 114
Отметьте правильный ответ
Линейное преобразование  задано матрицей
задано матрицей 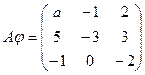 и вектор x=(1,1,
и вектор x=(1,1, 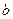 ) является собственным вектором преобразования
) является собственным вектором преобразования  . Найти
. Найти 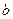 и
и 
£  =1,
=1, 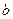 =1
=1
£  =2,
=2, 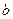 =-1
=-1
£  =1,
=1, 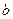 =-1
=-1
R  =2,
=2, 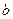 =1
=1
93. Задание {{ 115 }} ТЗ № 115
Отметьте правильный ответ
Линейное преобразование  задано матрицей
задано матрицей  . При каком значении
. При каком значении  ,
,  является собственным значением
является собственным значением 
£  =1
=1
£  =3
=3
R  =2
=2
£  =-1
=-1
94. Задание {{ 116 }} ТЗ № 116
Отметьте правильный ответ
Всякая матрица, все характеристические кони которой действительны и различны….
R приводится к диагональному виду
£ приводится к единичной матрице
£ является вырожденной
£ является невырожденной
95. Задание {{ 117 }} ТЗ № 117
Отметьте правильный ответ
Преобразование  задано матрицей
задано матрицей 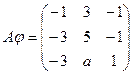 . Найти диагональный вид этой матрицы в некотором базисе.
. Найти диагональный вид этой матрицы в некотором базисе.
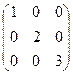
£ 
£ 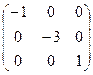
£ 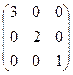
R  -не приводится к диагональному виду.
-не приводится к диагональному виду.
96. Задание {{ 118 }} ТЗ № 118
Отметьте правильный ответ
Построить ортогональный 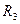 базис содержащий вектор
базис содержащий вектор 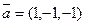
£ (2,-1,1)
(1,-1,1)
(-1,3,5)
R (1,-1,1)
(2,1,-1)
(0,1,1)
£ (1,-1,1)
(1,2,1)
(-2,1,1)
£ (1,1,-1)
(0,1,0)
(1,-1,0)
97. Задание {{ 119 }} ТЗ № 119
Отметьте правильный ответ
Найти вектор, дополняющий систему 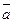 =(2/3,1/3,2/3),
=(2/3,1/3,2/3), 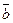 =(1/3,2/3,-2/3) до ортогонального базиса
=(1/3,2/3,-2/3) до ортогонального базиса
£ (2/3,2/3,-1/3)
£ (-2/3,2/3,1/3)
£ 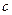 =(2,-2,-1)
=(2,-2,-1)
R 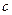 =(2/3,-2/3,-1/3)
=(2/3,-2/3,-1/3)
98. Задание {{ 120 }} ТЗ № 120
Отметьте правильный ответ
Векторы 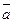 и
и 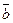 векторного пространства
векторного пространства 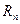 называются ортогональными, если…
называются ортогональными, если…
R 
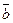 = 0
= 0
£ 
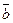 =
= 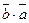
£ 
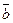 = -
= - 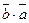
£ 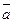 =
= 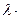
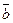
99. Задание {{ 121 }} ТЗ № 121
Отметьте правильный ответ
Пусть 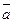 и
и 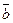 –векторы линейного пространства
–векторы линейного пространства 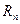 .Если
.Если  = 0, то…
= 0, то…
£ 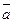 =0 или
=0 или 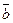 =0
=0
R 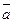 и
и 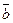 - ортогональны
- ортогональны
£ 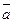 и
и 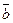 - линейно зависимы
- линейно зависимы
£ 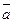 и
и 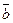 - линейно независим
- линейно независим
100. Задание {{ 122 }} ТЗ № 122
Отметьте правильный ответ
Если система ненулевых векторов 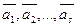 из
из 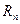 ортогональна, то она …
ортогональна, то она …
£ образует базис
£ линейно зависима
R линейно независима
£ содержит единичный вектор
101. Задание {{ 123 }} ТЗ № 123
Отметьте правильный ответ
Матрица перехода от ортонормированной базы евклидова пространства к любой другой его ортонормированной базе является …
R ортогональной матрицей
£ симметричной матрицей
£ единичной матрицей
£ вырожденной матрицей
102. Задание {{ 124 }} ТЗ № 124
Отметьте правильный ответ
Найти вектор, дополняющий систему векторов 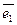 = (1,2,-1),
= (1,2,-1), 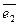 = (2,-1,0) до ортогонального базиса
= (2,-1,0) до ортогонального базиса
£ 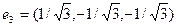
£ 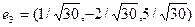
£  (1/3,2/3,0)
(1/3,2/3,0)
R 
103. Задание {{ 125 }} ТЗ № 125
Отметьте правильный ответ
Найти вектор, дополняющий систему векторов 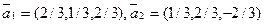 , до ортогонального базиса
, до ортогонального базиса
R 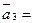 (2/3,-2/3,-1/3)
(2/3,-2/3,-1/3)
£ 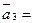 (2/3,2/3,-1/3)
(2/3,2/3,-1/3)
£ 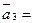 (2/3,-2/,1/3)
(2/3,-2/,1/3)
£ 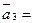 (1,-1,1)
(1,-1,1)
104. Задание {{ 126 }} ТЗ № 126
Отметьте правильный ответ
При каких значениях  и
и  векторы
векторы  и
и 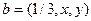 – ортогонормированны?
– ортогонормированны?
£  =1,
=1,  =-1
=-1
R 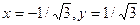
£  =0,
=0,  =1
=1
£  =1,
=1,  =0
=0
105. Задание {{ 127 }} ТЗ № 127
Отметьте правильный ответ
При каких целых значениях  и
и  векторы
векторы  и
и 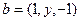 – ортогональны?
– ортогональны?
£ При любых целых  ,
, 
£  +
+  = -2
= -2
R  +
+  = 2
= 2
£  +
+  = 1
= 1
106. Задание {{ 128 }} ТЗ № 128
Отметьте правильный ответ
Применяя процесс ортогонализации построить ортогональный базис пространства, натянутого на систему векторов 
£ 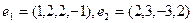
£ 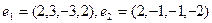
£ 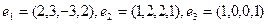
R 
107. Задание {{ 129 }} ТЗ № 129
Отметьте правильный ответ
Применяя процесс ортогонализации построить ортогональный базис пространства, натянутого на систему векторов 
£ 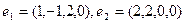
R 
£ 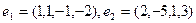
£ 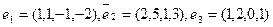
108. Задание {{ 130 }} ТЗ № 130
Отметьте правильный ответ
Применяя процесс ортогонализации к векторам 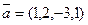 и
и  найти
найти 
R  = 1/5
= 1/5
£  = -1/5
= -1/5
£  = 5
= 5
£  = -5
= -5
109. Задание {{ 131 }} ТЗ № 131
Отметьте правильный ответ
Применяя процесс ортогонализации найти, при каком значении  векторы
векторы 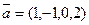 и
и 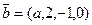 будут ортогональны, если
будут ортогональны, если  = -1/3
= -1/3
£  = 1
= 1
£  = 2
= 2
£  = 3
= 3
R  = 4
= 4
110. Задание {{ 132 }} ТЗ № 132
Отметьте правильный ответ
Применяя процесс ортогонализации построить ортогональный базис подпространства, натянутого на систему векторов 
£ 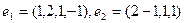
£ 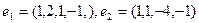
R 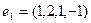
£ 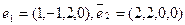
111. Задание {{ 133 }} ТЗ № 133
Отметьте правильный ответ
Если скалярное произведение векторов 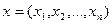 и
и 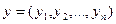 евклидова пространства равно
евклидова пространства равно 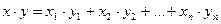 , то базис, в котором заданы координаты векторов, является…
, то базис, в котором заданы координаты векторов, является…
£ ортогональным
£ состоящим из векторов
£ состоящим из векторов
R ортонормированным
112. Задание {{ 134 }} ТЗ № 134
Отметьте правильный ответ
Линейное преобразование  евклидова пространства
евклидова пространства 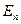 называется ортогональным преобразованием, если…
называется ортогональным преобразованием, если…
£ 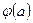 и
и  - ортогональны
- ортогональны
R 
£ 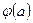 =
= 
£ существует  вектор, что
вектор, что 
113. Задание {{ 135 }} ТЗ № 135
Отметьте правильный ответ
Если при линейном преобразовании  евклидова пространства
евклидова пространства 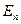
 сохраняется скалярный квадрат всякого вектора из
сохраняется скалярный квадрат всякого вектора из 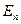 , то
, то  называется … преобразованием.
называется … преобразованием.
£ тождественным
£ симметричным
R ортогональным
£ единичным
114. Задание {{ 136 }} ТЗ № 136
Отметьте правильный ответ
Если линейное преобразование евклидова пространства переводит хотя бы одну ортонормированную базу в ортонормированную базу, то это преобразование...
R ортогонально
£ симметрично
£ тождественно
£ нулевое
115. Задание {{ 137 }} ТЗ № 137
Отметьте правильный ответ
Матрица ортогонального преобразования евклидова пространства в любой ортонормированной базе является…
£ скалярной матрицей
R ортогональной матрицей
£ единичной матрицей
£ диагональной матрицей
116. Задание {{ 138 }} ТЗ № 138
Отметьте правильный ответ
Линейное преобразование  n –мерного евклидова пространства называется симметрическим, если для любых векторов
n –мерного евклидова пространства называется симметрическим, если для любых векторов 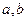 этого пространства верно равенство…
этого пространства верно равенство…
R 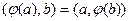
£ 
£ 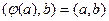
£ 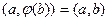
117. Задание {{ 139 }} ТЗ № 139
Отметьте правильный ответ
Матрица симметрического евклидова пространства в любой ортонормированной базе является …
£ ортогональной матрицей
£ единичной матрицей
£ скалярной матрицей
R симметрической матрицей
118. Задание {{ 140 }} ТЗ № 140
Отметьте правильный ответ
Все характеристические корни симметрического преобразования…
£ различна
£ целые
R действительны
£ равны
119. Задание {{ 141 }} ТЗ № 141
Отметьте правильный ответ
Собственные векторы симметрического преобразования, относящиеся к различным собственным значениям, между собой …
R пропорциональны
£ ортогональны
£ различны
£ равны
120. Задание {{ 142 }} ТЗ № 142
Отметьте правильный ответ
Если  – линейное преобразование евклидова пространства, сохраняющее длины всех векторов, то оно …
– линейное преобразование евклидова пространства, сохраняющее длины всех векторов, то оно …
£ симметрично
£ не существует
£ тождественно
R ортогонально
121. Задание {{ 143 }} ТЗ № 143
Отметьте правильный ответ
При каких значениях 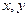 векторы
векторы 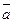 и
и 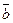 , где
, где  , образуют ортонормированную систему?
, образуют ортонормированную систему?
£ 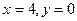
£ при любых 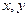
R ни при каких 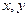
£ 
122. Задание {{ 144 }} ТЗ № 144
Отметьте правильный ответ
При каких значениях 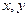 векторы
векторы 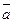 и
и 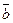 , где
, где 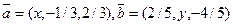 , образуют ортонормированную систему?
, образуют ортонормированную систему?
£ 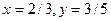
R ни при каких 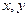
£ 
£ 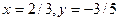
123. Задание {{ 145 }} ТЗ № 145
Отметьте правильный ответ
Базис  векторного пространства
векторного пространства 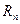 называется ортогональным, если…
называется ортогональным, если…
R 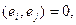

£ 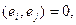
£ 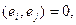
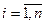
£ 

124. Задание {{ 146 }} ТЗ № 146
Отметьте правильный ответ
Как изменяется матрица линейного преобразования, если в базе  поменять местами два вектора
поменять местами два вектора 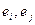 ?
?
£ в матрице поменяются местами i и j строки
£ в матрице поменяются местами i и j столбцы
£ в матрице i строка поменяется местами с j столбцом
R в матрице поменяются местами i и j строки и i и j столбцы
125. Задание {{ 147 }} ТЗ № 147
Отметьте правильный ответ
Линейное преобразование φ тогда и только тогда задается в базе  диагональной матрицей, если все векторы этой базы являются…
диагональной матрицей, если все векторы этой базы являются…
£ несобственными векторами преобразования  .
.
R собственными векторами преобразования  .
.
£ единичными
£ нулевыми
126. Задание {{ 148 }} ТЗ № 148
Отметьте правильный ответ
Линейное преобразование  тогда и только тогда задается в базе
тогда и только тогда задается в базе  … матрицей, если все векторы этой базы являются собственными векторами преобразования
… матрицей, если все векторы этой базы являются собственными векторами преобразования  .
.
£ скалярной
£ нулевой
£ единичной
R диагональной
127. Задание {{ 149 }} ТЗ № 149
Отметьте правильный ответ
Всякое линейное преобразование с простым спектром может быть задано…матрицей
R диагональной
£ скалярной
£ единичной
£ нулевой
128. Задание {{ 150 }} ТЗ № 150
Отметьте правильный ответ
Собственные векторы  линейного преобразования
линейного преобразования  , относящиеся к различным собственным значениям, составляют…
, относящиеся к различным собственным значениям, составляют…
£ базис
£ нелинейную систему векторов
R линейно независимую систему
£ линейно зависимую
129. Задание {{ 151 }} ТЗ № 151
Отметьте правильный ответ
Линейное преобразование  действительного линейного пространства
действительного линейного пространства  имеет простой спектр, если все его характеристические корни…
имеет простой спектр, если все его характеристические корни…
£ равны между собой
R действительны и различны
£ комплексны
£ равны нулю
130. Задание {{ 152 }} ТЗ № 152
Отметьте правильный ответ
Линейное преобразование  действительного линейного пространства
действительного линейного пространства  имеет …, если все его характеристические корни действительны и различны
имеет …, если все его характеристические корни действительны и различны
R простой спектр
£ нулевой вектор
£ базис
£ размерность
 2015-10-22
2015-10-22 786
786








