Коэффициент концентрации внимания Kk

Для определения оптимальной величины интервала h используют формулу Стерджеса:

,

где Кк_max, Кк_min-максимальное и минимальное значение коэффициента концентрации внимания в исследуемом вариационном ряду, с.;

N- общее число наблюдений. N=22.

h = 0,1 c;

V_ср = 1,002 сек.

Построение интервального вариационного ряда.

Таблица 6

Границы интервалов, с.	Середины интервалов Vci, с.	Опытные частоты, mi*	Опытные частости, Pi*	Накопленные частости, F(v)	mi* *Vci,	mi* *V2ci,	(Vci, - Vср)3 * Pi*	(Vci, - Vср)4 * Pi*
0,674-0,774	0,724		0,181818	0,181818	2,896	2,096704	-0,0038758	0,001075
0,774-0,874	0,824		0,090909	0,272727	1,648	1,357952	-0,0005064	0,000090
0,874-0,974	0,924		0,045455	0,318182	0,924	0,853776	-0,0000210	0,000002
0,974-1,074	1,024		0,363636	0,681818	8,192	8,388608	0,0000043	0,000000
1,074-1,174	1,124		0,090909	0,772727	2,248	2,526752	0,0001680	0,000021
1,174-1,274	1,224		0,227273		6,12	7,49088	0,0025111	0,000559
Сумма	-				22,028	22,71467	-0,00171976	0,00174606

Рисунок 5 - Интервалы Кк

значение Кк студента Соковой входит в третий интервал.

Из графика видно, что данное распределение близко к нормальному.

Рассчитаем статистические параметры:

Математическое ожидание:

=

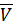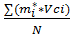
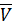_кк = 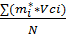= = 1,001 сек;

Статическая дисперсия:

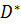(V) = - ;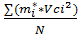

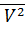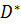(V)_кк= 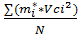- 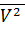= - =0,0299;

Несмещенная оценка дисперсии:

D(V) = * (V)_кк;

D(V)_кк = 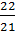*0,0299= 0,0314;

Стандартное среднеквадратическое отклонение:

= ;

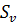= = 0,177 сек;

Коэффициент вариации:

ν= 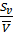*100%;

ν_кк= * 100% =17,69%;

Коэффициент вариации характеризует относительную меру отклонения измеренных значений от среднеарифметического:

В данном случае коэффициент вариации менее 33%, что говорит об однородности информации.

Асимметрия:

= ∑ * ;

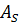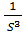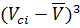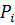A_sкк = *(- 0,00172) = - 0,3096;

В данном случае распределение левостороннее.

Эксцесс:

EK= 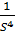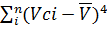*Pi – 3;

EK_кк = * 0,001746– 3 = -1,22;

Показатель эксцесса характеризует степень колеблемости исходных данных.

Поскольку коэффициент эксцесса меньше нуля, то данный график распределения имеет более плоскую вершину.