Объем цилиндрического тела

Рассмотрим тело, ограниченное сверху поверхностью , снизу – замкнутой областью D плоскости Оху, боковое ограничение- цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см.рис.2.1).

Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z=f(x;y) на плоскость Оху) произвольным образом на n областей , площади которых равны . Рассмотрим цилиндрические столбики с основаниями , ограниченные сверху кусками поверхности z=f(x;y). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием через , получим.

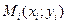Возьмем на каждой площадке произвольную точку и заменим каждый столбик прямым цилиндром с тем же основанием и высотой 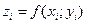. Объем этого цилиндра приблизительно равен объему цилиндрического столбика, т.е. . Тогда получаем:

Это равенство тем точнее, чем больше число n и чем меньше размеры «элементарных областей» . Естественно принять предел суммы при условии, что число площадок неограниченно увеличивается , а каждая площадка стягивается в точку (), за объем V цилиндрического тела, т.е. , или, согласно равенству .

Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела.