2015-10-22
2319
Дискретная математика
Методические указания и контрольные задания для студентов I курса заочной формы обучения
Оглавление
I. Краткие теоретические сведения. 2
I.1. Множества и операции над ними. 2
I.2. Бинарные отношения. 5
1. Отношение эквивалентности. 7
2. Отношение упорядоченности. 8
3. Функции. 10
I.3. Функции и формулы алгебры логики. 11
I.4. Двойственные функции и совершенные нормальные формы.. 19
1. Принцип двойственности. 19
2. Построение совершенных нормальных форм. 20
I.5. Полнота и замкнутость систем функций алгебры логики. 26
1. Полные системы функций алгебры логики. 26
2. Важнейшие замкнутые классы.. 27
II. Задание к контрольной работе по дискретной математике. 32
III. Варианты контрольных работ. 34
IV. Пример решения контрольной работы.. 59
V. Список литературы.. 75
I. Краткие теоретические сведения
I.1. Множества и операции над ними
Множество – понятие интуитивное, и поэтому не имеет точного математического определения. Под множеством обычно понимают совокупность определенных и хорошо различимых объектов, которые рассматриваются как единое целое. Объекты, составляющие множество, называются его элементами. Тот факт, что x является элементом множества M, записывается так: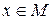 
, где символ 
обозначает отношение принадлежности элемента множеству. Если x не является элементом множества M, то пишут: 
.
|
|
|
Два множества A и B называются равными, если они состоят из одних и тех же элементов, таким образом, 
тогда и только тогда, когда 
и 
. Символом 
обозначается отношение включения множеств, т.е. 
означает, что . В этом случае A называется подмножеством B, а B – надмножеством A. Если 
и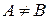 
, то A называется собственным подмножеством B, и в этом случае пишут: 
. Множество может состоять из конечного числа элементов (любого) или быть бесконечным. Множество, не содержащее элементов, называется пустым, и обозначается Æ. Множество множеств называют системой или семейством множеств.
Для записи множеств используется один из способов: а) перечисление элементов, например: 
, или б) указание свойств элементов, например: 
.
Объединением двух множеств A и B (или теоретико-множественной суммой) называется множество, состоящее из всех элементов, являющихся элементами хотя бы одного из множеств A или B. Таким образом, 
.
Объединением системы множеств 
называется множество 
.
Для графического изображения операции объединения множеств используются диаграммы Эйлера-Венна, где множества представлены как замкнутые области, а результат операции показан заштрихованной частью (см. рис.1).
Пересечением двух множеств A и B (или теоретико-множественным произведением) называется множество элементов, принадлежащих одновременно и A, и B. Таким образом, 
и 
.
|
|
|
Диаграмма Эйлера-Венна для пересечения двух множеств показана на рис.2.
Пересечением системы множеств называется множество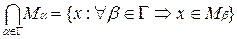 
.
Относительным дополнением множества B до множества A (или теоретико-множественной разностью) называется множество тех элементов A, которые не являются элементами B, таким образом, A \ B 
и 
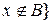. Диаграмма на рис.3.
Абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, таким образом, 
или 
U \ A, где U – некоторое универсальное множество, которое является надмножеством любого множества, рассматриваемого в данном рассуждении. Диаграмма на рис.4.
Симметрической разностью двух множеств A и B называется объединение двух разностей A \ B и B \ A, т.е. A Å B= (A \ B) 
(B \ A). Диаграмма на рис.5.
Декартовым (прямым) произведением двух множеств A и B называется множество всех упорядоченных пар (a,b)таких, что 
и 
, таким образом, 
и 
.
Декартовым (прямым) произведением множеств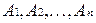 
называется множество всех упорядоченных последовательностей 
– «энок» таких, что 
, т.е. 
.
Если 
, то множество 
называется прямой степенью множества A и обозначается An.
Множества A и B в прямом произведении А ´ В называют координатными осями, а элементы x Î А и y Î В – проекциями вектора z =(x, y)Î А ´ В на координатные оси или координатами точки z (абсциссой и ординатой соответственно). Будем обозначать их пр А z и пр В z.
Пусть множество М Ì А ´ В, проекцией множества М на ось А называется множество всех абсцисс векторов из М, проекцией множества М на ось В называется множество всех ординат векторов из М, т.о. пр А М ={ пр А z: z Î М }={ x Î А: $ y Î В и (x, y)Î М } и пр В М ={ пр В z: z Î М }={ y Î В: $ x Î А и (x, y)Î М }.
Для многомерного случая A 1 ´ A 2 ´ A 3 ´ …´ An, каждое множество Ai называется i- той координатной осью. Проекция вектора z =(a 1, a 2,…, an) на i -тую координатную ось равна его i- той координате: пр i z = ai, где i =1,2,…, n. Если М Ì A 1 ´ A 2 ´…´ An, то пр i М ={ пр i z: z Î М }. Определены также проекции вектора z и множества векторов М на несколько координатных осей с номерами i 1, i 2,…, ik: пр i 1, i 2… ik z = (ai 1, ai 2,…, aik) – k ‑мерный вектор и пр i 1, i 2… i k М = { пр i 1, i 2… i k z: z Î М } – множество k ‑мерных векторов.
Пример:
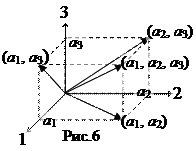Тройки вещественных чисел (а 1, а 2, а 3) можно рассматривать как точку в трехмерном пространстве (или вектор, проведенный в эту точку из начала координат). Тогда пр i (а 1, а 2, а 3)= ai, где i =1,2,3, пр i,j (а 1, а 2, а 3)=(ai, aj), где i,j =1,2,3. См. рис.6.
