2015-10-22
631
В некоторых случаях для описания случайного процесса применяют его представление через сумму случайных процессов более простого вида. Один из способов такого представления называется каноническим разложением [32]. При каноническом разложении случайный процесс представляют в виде
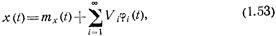
где mx(t) —математическое ожидание процесса; 
— координатные функции, являющиеся заданными неслучайными функциями времени; Vi — коэффициенты, являющиеся некоррелированными случайными величинами с нуле выми математическими ожиданиями и дисперсиями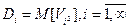 
.
В качестве координатных функций в канонических разложениях используют семейства функций, обладающих свойством ортонормированности:
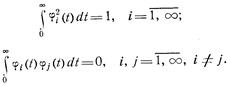
Корреляционная функция случайного процесса (1.53) выражается через его каноническое разложение так:
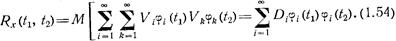
Суммирование по переменной R исчезает, поскольку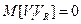 
вследствие некоррелированности случайных величин 
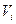и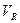 
.
Полагая t1 = t2=t, из (1.54) получаем выражение для дисперсии
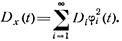
При практических расчетах ограничиваются конечным числом членов канонического разложения. Методика построения канонических разложений случайных процессов изложена в книге [32].
