Скалярные случайные поля

Обозначим вектором х= {х, у, z} вектор аргументов про­странственного скалярного случайного поля и(х). Вектор х опреде­лен в области D возможного изменения координат х, у, z. Точку назовем точкой наблюдения поля. В каждой точке скаляр­ного поля наблюдается скалярная случайная величина .

Скалярное случайное поле и(х) считается описанным полностью, если для произвольного числа точек наблюдения известен способ построения «-мерного совместного безусловного распреде­ления вероятностей системы случайных величин .

В частности, если при любых , и любом п справедливо соотношение

то поле и(х) называется абсолютно случайным, и для его описания достаточно задать зависимость одномерной плотности р_u(х) от ко­ординат х точки наблюдения этого поля.

Как и при описании случайных величин и процессов, для описа­ния случайных полей часто пользуются их моментными характерис­тиками.

n-точечным начальным моментом порядка t_i +... + i_n скалярно­го поля и(х) называется математическое ожидание произведения соответствующих степеней возможных значений поля в n точках наблюдения:

Одноточечный начальный момент первого порядка

называется математическим ожиданием скалярного случайного поля. Оно характеризует среднее значение случайной величины и в каждой точке х области D.

Разность есть центрированное случайное поле. Среднюю величину произведения степеней возмож­ных значений центрированного поля в n точках наблюдения называют «-точечным центральным моментом порядка :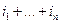

Одноточечный центральный момент второго порядка

есть дисперсия скалярного поля u(х), а двухточечный центральный момент второго порядка

— его корреляционная функция. Дисперсия случайного поля харак­теризует рассеивание случайных значений поля в точке наблюде­ния, а корреляционная функция — корреляцию значений поля в двух его точках наблюдения х₁ и х₂.

Скалярное случайное поле может обладать свойствами однород­ности и изотропности. Поле и(х) называется однородным (строгая однородность), если его n -точечное совместное распределение не изменяется при переносе точек наблюдения этого поля на один и тот же вектор х₀, т. е.

при любом х₀ и любом числе точек наблюдения п.

Скалярное случайное поле u(х) называется однородным в широ­ком смысле, если его математическое ожидание т_u(х) является постоянным во всех точках области D, а корреляционная функция не изменяется при переносе пары точек наблюдения х₁ и х₂ на один и тот же вектор х₀, т. е.

(1.69)

Иными словами, аргументом корреляционной функции однородно­го скалярного поля являются не координаты х₁ и х₂ точек наблю­дения этого поля, а вектор соединяющий эти точки в области D. Свойство однородности скалярного случайного поля эквивалентно свойству стационарности случайного процесса.

Однородное скалярное поле u(х) называется изотропным, если корреляция между значениями этого поля в точках х₁ и х₂ не зави­сит от ориентации вектора , а зависит только от его длины . Таким образом, в рамках корреляционной теории изотропное скалярное случайное поле u(х) описывается двумя ха­рактеристиками: математическим ожиданием m_u(x) =const и кор­реляционной функцией R_u(r).