Векторные случайные поля

Рассмотрим векторное пространственное случайное по­ле и(х), у которого аргумент х - вектор с координатами х, у, z, принадлежащий области наблюдения поля D, а и — вектор с проек­циями и_х, и_у, u_z.

Проекции и_х(х), и_у(х), u_z(x) можно рассматривать как совокуп­ность трех случайных полей. Статистическое описание этой совокуп­ности эквивалентно статистическому описанию векторного поля и(х). В рамках корреляционной теории для описания совокупности скалярных случайных полей и_х(х), и_у(х) и u_z(x) требуется задать вектор их математических ожиданий т_и(х) и матричную корреля­ционную функцию . Вектор математических ожиданий со­стоит из трех компонент , каждая из которых есть математическое ожидание соответствующей со­ставляющей вектора и в точке наблюдения х.

Матричная корреляционная функция характеризует статистическую взаимосвязь между различными компонентами век­тора и в двух различных точках наблюдения поля х₁ и х₂ в облас­ти D:

где

Если поле ы(х), у которого аргумент х состоит из трех компо­нент х, у, z, содержит три компоненты и_х, и_у, и_z, то матричная кор­реляционная функция имеет размерность 3×3. Элементы , и — автокорреляционные функции составляющих и_х, и_у и и_z векторного поля; остальные эле­менты— взаимные корреляционные функции между различными составляющими этого поля. Например, корреляция между компо-

нентами и_х и и_у в точках наблюдения х₁ и х₂ характеризуется вза­имной корреляционной функцией

где

При х₁-х₂=х, т. е. при совпадении двух точек наблюдения, матричная корреляционная функция векторного случай­ного поля u(х) обращается в его корреляционную матрицу K_u(x), диагональными элементами которой являются дисперсии составля­ющих и_х, и_у, u_z вектора и в точке х, а внедиагональными — взаим­ные корреляционные моменты этих составляющих.

Как и скалярное, векторное случайное поле может быть одно­родным и изотропным. Статистические характеристики однородно­го векторного случайного поля u(х) инвариантны относительно па­раллельного переноса точек наблюдения поля в области D на оди­наковый вектор х₀ произвольной длины. Для такого поля математи­ческое ожидание есть постоянный вектор , a матричная корреляционная функция зависит только от вектора соединяющего точки наблюдения х₁ и х₂, и не зависит от положения точки х₁ начала вектора в области D.

Для рассмотрения свойства изотропности однородного вектор­ного пространственного случайного поля введем две системы коор­динат: абсолютную (неподвижную) и подвижную. Однородное векторное случайное поле называется изотропным, если его момент-ные характеристики инвариантны не только по отношению к парал­лельным переносам точек наблюдения поля, но также относительно их произвольных вращений и зеркальных отображений совместно с вращениями и зеркальными отображениями осей подвижной систе­мы координат относительно абсолютной системы координат.

Из определения свойства изотропности однородного векторного случайного поля следует, что такое поле должно иметь нулевой век­тор математических ожиданий , а матричная корреляцион­ная функция R_u(r), где , должна быть диаго­нальной. Все взаимные корреляционные функции, входящие в R_u(r), равны нулю. Одна из трех ненулевых автокорреляционных функций изотропного векторного поля характеризует корреляцию между проекциями и_r(х₁) и и_r(х₂) вектора u(х) на вектор r, соединяющий две рассматриваемые точки наблюдения поля. Эту автокорреляци­онную функцию изотропного поля R_r(r) =M[u_r(x), u_r(x + r)] назы­вают продольной. Две другие автокорреляционные функции и изотропного поля одинаковы: 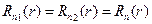. Каж­дая из них характеризует корреляцию между параллельными проек­циями и_n(х) и и_n(х+r), перпендикулярными вектору г, в точках х и x+r:

Таким образом, для полного описания изотропного векторного случайного поля в трехмерном пространстве в рамках корреляцион­ной теории требуется задать две его корреляционные функции: u .

От матричной корреляционной функции R_u(r) изотропного век­торного случайного поля и(х) можно перейти к матричной спек­тральной плотности этого поля. Как и R_u(r), матричная спектральная плотность есть квадратная диагональная мат­рица 3×3 с элементами

Аргументом в спектральных плотностях и 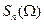явля­ется волновое число, размерность которого обратна размерности r.