Стационарные случайные процессы (слабая стационарность)

Случайный процесс x(t) (скалярный или векторный), у которого математическое ожидание m_x(t) постоянно, а корреляционная функция зависит не от самих значений аргументов t₁ и t₂, а от их разности , т. е. , назы­вают слабо стационарным случайным процессом, или стационар­ным в широком смысле.

Дисперсия стационарного случайного процесса D_x = R_x(0) по­стоянна. Интервал , за пределами которого корреляционная функция не превосходит некоторую установленную малую ве­личину, называют временем корреляции процесса x(t). Величина является простейшей количественной мерой степени коррелиро­вания значений случайного процесса по времени.

Эргодическое свойство. Для определения математического ожи­дания и корреляционной функции стационарного случайного про­цесса по экспериментальным данным следует пользоваться формулами математической статистики, подставляя в них значения различных реализаций процесса в соответствующие моменты време­ни. Однако в некоторых случаях результаты расчетов не изменятся, если в эти формулы подставлять значения одной достаточно длинной реализации случайного процесса x(t) в различные моменты времени. Про стационарные случайные процессы, для кото­рых такая замена справедлива, говорят, что они обладают эргодическим свойством.

Необходимым и достаточным условием эргодичности стационар­ного случайного процесса является выполнение равенства [32]

а достаточным — выполнение более простого условия

Для расчета математического ожидания т_х и корреляционной функции стационарного случайного процесса x(t), обладаю­щего свойством эргодичности, можно пользоваться соотношениями

где - одна длинная реализация процесса.

При проведении расчетов на ЦВМ эти интегралы заменяют ко­нечными суммами

Белый шум. Так, в рамках корреляционной теории определяют случайный процесс x(t), значения которого x(t₁) и x(t₂) некоррели-рованы при сколь угодно малом . Можно показать [32], что некоррелированность значений случайного процесса x(t) в мо­менты t₁ и t₂ при сколь угодно малом может быть обеспе­чена лишь в том случае, когда его корреляционная функция 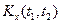имеет вид

где 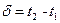- дельта-функция в точке t = t₁.

Множитель N(t₁) называют интенсивностью белого шума, кото­рая определяется как предел

У стационарного белого шума интенсивность N постоянна во времени. Если N=1, то стационарный белый шум называют стан­дартным. Из определения дельта-функции следует, что дисперсия белого шума D_x(t) =R_x(t, t) равна бесконечности. Это означает, что физически белый шум не может быть реализован точно и может рассматриваться лишь как абстракция — результат предельного перехода коррелированного случайного процесса при .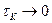

Векторный белый шум x(t), состоящий из п компонент, характе­ризуется матрице» интенсивностей N(t) = [N_ij(t)]n×n. Диагональ­ные элементы , этой матрицы суть интенсивности от­дельных составляющих векторного белого шума, а внедиагональные - взаимные интенсивности, характеризующие корреля­цию между различными составляющими векторного белого шума в один и тот же момент времени. Наиболее часто рассматривают случай, когда все составляющие векторного белого шума некорре­лированные. В этом случае матрица N(t) диагональная.

Понятие белого шума находит широкое применение при решении многих задач статистического анализа и оптимизации управления движением летательных аппаратов.