В тех случаях, когда управляемое движение летательного аппарата, происходящее при воздействии случайных возмущений, описывается нелинейными уравнениями, распределения вероятностей фазовых координат оказываются негауссовскими. Это усложняет задачу анализа точности нелинейных систем и является причиной отсутствия единого универсального метода ее решения.
В данном разделе рассматривается приближенный метод статистического анализа стохастических систем, называемый методом статистической линеаризации. В его основу положены использование принципа статистической линеаризации для замены нелинейных звеньев исследуемой системы эквивалентными им в статистическом смысле линейными соотношениями и применение частотного метода для анализа точности результирующей статистически линеаризованной системы.
Принцип статистической линеаризации. Рассмотрим нелинейное соотношение

где х и у — скалярные случайные процессы.
Заменим это соотношение следующим:

Входящие в (2.32) статистическая характеристика нелинейности Фо и статистический коэффициент усиления К — неслучайные функции;  —центрированный случайный процесс.
—центрированный случайный процесс.
Характеристику 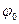 и коэффициент К выбирают так, чтобы процессы y(t) и z(t) были статистически эквивалентны друг другу. Критерии эквивалентности могут быть различными. Каждый из них определяет способ расчета характеристики
и коэффициент К выбирают так, чтобы процессы y(t) и z(t) были статистически эквивалентны друг другу. Критерии эквивалентности могут быть различными. Каждый из них определяет способ расчета характеристики 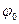 и коэффициента К. В практике расчетов наиболее широкое распространение нашли следующие два способа замены нелинейности
и коэффициента К. В практике расчетов наиболее широкое распространение нашли следующие два способа замены нелинейности  соотношением (2.32).
соотношением (2.32).
Первый способ. Требуется выполнение двух равенств: my = mz
и Dy = Dz. Поскольку  , то
, то

Из равенства Dy = Dz с учетом  и
и  получаем соотношение для расчета коэффициента:
получаем соотношение для расчета коэффициента:

Второй способ. При этом способе 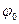 и К определяются из условия минимума среднего квадрата ошибки аппроксимации
и К определяются из условия минимума среднего квадрата ошибки аппроксимации

Поскольку
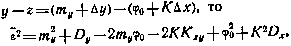
где Кxy — взаимный корреляционный момент переменных х и у.
Необходимыми условиями экстремума  по
по 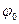 и К являются равенства
и К являются равенства

откуда

а

Поскольку 
то окончательное выражение для К имеет вид

Можно показать, что при определении 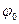 и К(2) с помощью соотношений (2.35) и (2.36) критерий
и К(2) с помощью соотношений (2.35) и (2.36) критерий  достигает именно минимума [32]. Отметим, что характеристика
достигает именно минимума [32]. Отметим, что характеристика 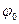 при первом и втором способах аппроксимации рассчитывается с помощью одного и того же соотношения (2.35).
при первом и втором способах аппроксимации рассчитывается с помощью одного и того же соотношения (2.35).
Полученные формулы позволяют найти зависимость вида (2.32), эквивалентную заданной нелинейной зависимости  в соответствии с выбранным критерием. Для этого должно быть известно одномерное распределение р(х) входного воздействия x(t).
в соответствии с выбранным критерием. Для этого должно быть известно одномерное распределение р(х) входного воздействия x(t).
Когда нелинейное звено  является элементом замкнутой динамической системы, распределение р(х) может быть произвольным и при расчете
является элементом замкнутой динамической системы, распределение р(х) может быть произвольным и при расчете 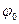 и К не известно. Однако если учесть свойство нормализации, заключающееся в том, что распределения вероятностей выходных переменных инерционных звеньев замкнутой нелинейной динамической системы близки к гауссовскому даже при негауссовских распределениях их входных переменных [32], то распределение р(х) переменной на входе нелинейности
и К не известно. Однако если учесть свойство нормализации, заключающееся в том, что распределения вероятностей выходных переменных инерционных звеньев замкнутой нелинейной динамической системы близки к гауссовскому даже при негауссовских распределениях их входных переменных [32], то распределение р(х) переменной на входе нелинейности  , находящейся после инерционного звена замкнутой системы, можно приближенно считать гауссовским. В этом допущении и заключается приближенность метода статистической линеаризации.
, находящейся после инерционного звена замкнутой системы, можно приближенно считать гауссовским. В этом допущении и заключается приближенность метода статистической линеаризации.
Если в соотношениях (2.33), (2.35) и (2.36) плотность распределения р(х) предположить гауссовской, то входящие в них несобственные интегралы могут быть вычислены или сведены к интегралу Лапласа и получены выражения для величин  и
и 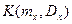 как функции математического ожидания тх и дисперсии Dx воздействия x(t) на входе нелинейности.
как функции математического ожидания тх и дисперсии Dx воздействия x(t) на входе нелинейности.
Вычисление статистического коэффициента усиления К(2) можно упростить, воспользовавшись соотношением

справедливым при гауссовском распределении входного воздействия, поскольку в этом случае

В случаях, когда  —однозначная нечетная нелинейная функция, статистическая характеристика
—однозначная нечетная нелинейная функция, статистическая характеристика  может быть представлена в виде выражения
может быть представлена в виде выражения

Коэффициент  называют статистическим коэффициентом усиления по математическому ожиданию входного воздействия x(t).
называют статистическим коэффициентом усиления по математическому ожиданию входного воздействия x(t).
Пример. Для реле с уровнем насыщения А, учитывая результаты, полученные в примере, рассмотренном в разд. 1.1, и формулы (2.35) и (2.33), имеем

а учитывая (2.40) и (2.37), получаем

Формулы для статистических коэффициентов усиления некоторых типовых нелинейных звеньев приведены в приложении 3.
Принцип статистической линеаризации может быть применен и в случае, когда процесс x(t) на входе нелинейности  векторный. Аппроксимирующая линейная зависимость приобретает вид
векторный. Аппроксимирующая линейная зависимость приобретает вид

Аргументами функций 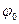 и
и 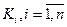 , в многомерном случае являются вектор математических ожиданий тх и корреляционная матрица Кх случайного вектора x(t).
, в многомерном случае являются вектор математических ожиданий тх и корреляционная матрица Кх случайного вектора x(t).
В выражении (2.42)
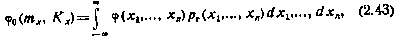
а коэффициенты Ki (при втором способе статистической линеаризации) рассчитываются по формуле

Статистический анализ нелинейных систем. В сочетании с частотным методом статистического анализа принцип статистической линеаризации образует метод статистического анализа стационарных нелинейных систем в установившемся режиме, называемый методом статистической линеаризации.
Рассмотрим нелинейную систему, структурная схема которой приведена на рис. 2.2. Система состоит из стационарной линейной части, описываемой передаточной функцией W(p), и нелинейности  в обратной связи, которую полагаем нечетной и однозначной.
в обратной связи, которую полагаем нечетной и однозначной.

Рис. 2.2. Структурная схема нелинейной системы
Входное воздействие системы u(t) — стационарный случайный процесс с известными математическим ожиданием тu и спектральной плотностью  . Требуется определить математическое ожидание тх и дисперсию Dx процесса x(t) на выходе системы в установившемся режиме.
. Требуется определить математическое ожидание тх и дисперсию Dx процесса x(t) на выходе системы в установившемся режиме.
Применяя принцип статистической линеаризации, заменим нелинейную функцию ср(х) эквивалентной зависимостью

Выражения для  и
и 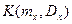 могут быть получены применительно к рассматриваемой нелинейности
могут быть получены применительно к рассматриваемой нелинейности  при помощи формул (2.35), (2.36) или (2.33) в соответствии с избранным способом статистической линеаризации или взяты из таблицы.
при помощи формул (2.35), (2.36) или (2.33) в соответствии с избранным способом статистической линеаризации или взяты из таблицы.
В результате такой замены получаем статистически-линеаризованную систему, для. которой в установившемся режиме
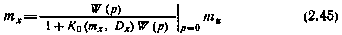
И
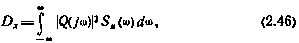
где

— частотная характеристика замкнутой линеаризованной системы, связывающей 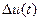 c
c  .
.
Если произведение  является рациональной дробью, выражение для интеграла (2.46) может быть найдено с помощью формулы (2.28). В результате получаем систему из четырех трансцендентных уравнений, первые два которой суть выражения для коэффициентов
является рациональной дробью, выражение для интеграла (2.46) может быть найдено с помощью формулы (2.28). В результате получаем систему из четырех трансцендентных уравнений, первые два которой суть выражения для коэффициентов 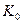 и К, а два другие — соотношения для тх и Dx в зависимости от
и К, а два другие — соотношения для тх и Dx в зависимости от 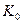 и К. Эту систему можно решить методом последовательных приближений или графически. В результате решения одновременно с тх и Dx определяются и коэффициенты
и К. Эту систему можно решить методом последовательных приближений или графически. В результате решения одновременно с тх и Dx определяются и коэффициенты 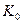 и К.
и К.
Если в решаемой задаче рассматриваемый выход системы y(t) не совпадает с входом x(t) нелинейности  , то задачу анализа точности системы приходится решать в два этапа. На первом этапе в качестве выхода рассматривается переменная x(t), и по изложенной схеме находятся коэффициенты
, то задачу анализа точности системы приходится решать в два этапа. На первом этапе в качестве выхода рассматривается переменная x(t), и по изложенной схеме находятся коэффициенты 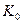 и К. На втором этапе, используя полученные значения коэффициентов
и К. На втором этапе, используя полученные значения коэффициентов 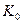 и К, с помощью частотного метода определяем искомые характеристики ту и Dy выхода системы y(t).
и К, с помощью частотного метода определяем искомые характеристики ту и Dy выхода системы y(t).

Рис. 2.3. Структурная схема нелинейного рулевого привода
Пример. Рассмотрим применение метода статистической линеаризации для анализа точности нелинейного рулевого привода с жесткой обратной связью [21]. Структурная схема привода, составленная с учетом ряда упрощений, показана на рис. 2.3. Предположим, что входное воздействие u(t) является стационарным случайным процессом с  и
и  .
.
Требуется определить  и
и  угла поворота рулей
угла поворота рулей  . Вначале в качестве выхода рассматриваем переменную х. В установившемся режиме
. Вначале в качестве выхода рассматриваем переменную х. В установившемся режиме

Дисперсия Dx определится из соотношения (2.46), где 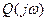 —частотная характеристика, соответствующая передаточной функции
—частотная характеристика, соответствующая передаточной функции

Для нелинейности типа «насыщение» с уровнем насыщения С при тх =0

С учетом указанного выражения для 

где 
Сводя интеграл (2.49) к  , получаем
, получаем

Систему уравнений (2.48) и (2.50) можно решить методом последовательных приближений, задав в качестве начального приближения  . Совместно с Dx из решения находим
. Совместно с Dx из решения находим 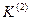 .
.
При полученной величине 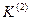 имеем
имеем

где  .
.
Определив интеграл с помощью  , окончательно находим
, окончательно находим

В установившемся режиме

 2015-10-22
2015-10-22 2297
2297








