Метод переходной матрицы

В ряде случаев статистический анализ управляемого дви­жения ЛА проводят, рассматривая линеаризованные уравнения воз­мущенного движения ЛА в нормальной форме Коши:

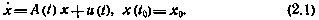
В этом уравнении X —вектор состояния (фазовый вектор), состоя­щий из п компонент; A(t) — динамическая матрица системы, имею­щая размерность п×п; u(t) — вектор входных (управляющих и воз­мущающих) воздействий системы размерности п.

Переменные, рассматриваемые при статистическом анализе в качестве выходных, не обязательно совпадают с компонентами фазового вектора системы. В общем случае вектор выходных координат y(t) размерности k связан с фазовым вектором x(t) и век­тором входных воздействий u(t) линейным соотношением

в котором Е(1) и D(t) —матрицы размерности k×n.

Переходная матрица. Уравнению (2.1) может быть поставлена в соответствие переходная матрица 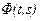, характеризующая дина­мические свойства рассматриваемой системы. Элементами переход­ной матрицы являются переходные функции 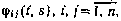, свя­зывающие единичное импульсное воздействие на систему по коор­динате в момент s с реакцией системы на это воздействие по ко­ординате в момент . Переходную матрицу 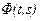, соответ­ствующую фиксированному моменту s, находят, рассматривая од­нородное уравнение

соответствующее уравнению (2.1), в котором вектор х заменен век­тором . Уравнение (2.3) интегрируют п раз, задавая в качестве начальных условий векторы . Получают п линейно независимых вектор-функций , которые, будучи собранными вместе, образуют переходную матрицу .

В матричной форме определение переходной матрицы 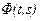, соответствующей фиксированному моменту , записывается как интегрирование обыкновенного дифференциального уравнения

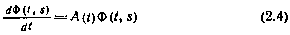
при начальном условии , где — единичная матрица размерности п.

Как функция меняющегося аргумента s при фиксированном мо­менте 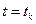наблюдения реакции системы, переходная матрица 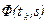может быть найдена путем интегрирования матричного уравнения, сопряженного к уравнению (2.4) [13, 4].

С использованием переходной матрицы 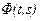общее решение системы (2.1) записывается так [4]:

Здесь первое слагаемое характеризует реакцию системы на на­чальное условие , второе — на внешнее воздействие u(s) при .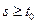

Если матрица А динамической системы — постоянная, т. е. сама система — стационарная, то переходная матрица 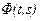такой си­стемы зависит только от разности аргументов , т. е. . Для стационарной системы существенным явля­ется только интервал времени между моментами s прило­жения воздействия к системе и t наблюдения ее реакции .

Корреляционная функция фазового вектора. Соотношение (2.5) позволяет определить вектор математических ожиданий m_x(t) и матричную корреляционную функцию , если 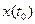— слу­чайный вектор, характеризуемый вектором математических ожиданий и корреляционной матрицей , a u(t) —векторный случайный процесс, характеризуемый математическим ожиданием и матричной корреляционной функцией .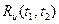

Применение к (2.5) операции математического ожидания дает

Вычитая почленно (2.6) из (2.5), получаем соотношение для цент­рированного вектора:

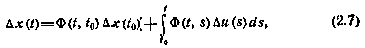
где .

По определению 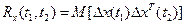. Предполагая и u(t) некоррелированными, в результате необходимых выкладок с использованием (2.7) получаем

При t₁ = t₂ = t из (2.8) получаем выражение для корреляционной матрицы фазового вектора:

Пример. В проекциях на оси орбитальной системы координат OXY компла­нарное относительное движение двух космических летательных аппаратов, один из которых (пассивный) движется по круговой орбите вокруг Земли, а второй (активный) сближается с первым (рис. 2.1), может быть описано следующей системой линейных дифференциальных уравнений [34]:

где — орбитальная угловая скорость пассивного ЛА; а_х и a_y — проекция уп­равляющего ускорения активного ЛА на оси системы OXY.

Рис. 2.1. К примеру анализа точности относительного движения ЛА

Предположим, что управление тра­екторией активного ЛА происходит импульсно и что последний перед встречей импульс скорости V_K прикладывается в момент t₀. При коррекции имеют место случайные ошибки реализации коррек­тирующего импульса. Требуется опреде­лить корреляционную матрицу случайных отклонений ЛА в относительном движении по положению и скорости в мо­мент , полагая ошибки реализации корректирующего импульса по со­ставляющим V_x и V_v независимыми, характеризуемыми дисперсиями _и .

Решение задачи начнем с определения переходной матрицы 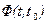, соот­ветствующей системе (2.10). Для этого перепишем систему (2.10) в виде век­торного линейного уравнения

х = Ах, (2.11)

в котором

Составив уравнение вида (2.4), соответствующее (2.11) и (2.12), и решив его аналитически при начальном условии , получаем следующие элементы матрицы :

В рассматриваемой постановке задачи корреляционная матрица K_x(t₀) обусловлена только дисперсиями ошибок реализации корректирующего импуль­са скорости, поэтому

где

Подстановка (2.14), а также 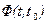и в первую часть формулы (2.5) дает искомую корреляционную матрицу .Второе слагаемое в формуле (2.5) в данном случае равно нулю, поскольку считается, что возмуще­ния, действующие на аппараты в период , отсутствуют. Элементы матрицы характеризующие отклонения аппаратов по положению, равны

Если входное воздействие u(t) является стационарным случай­ным процессом с корреляционной функцией , а система (2.1) стационарна и устойчива, то в установившемся режиме по оконча­нии переходного процесса, вызванного начальными условиями, век­тор состояния системы x(t) также будет стационарным случайным процессом. Матричная корреляционная функция этого про­цесса уже не зависит от корреляционной матрицы случай­ного вектора начальных условий :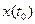

Переходя в (2.15) к переменным , и ,получаем выражение для матричной корреляционной функции фа­зового вектора устойчивой стационарной линейной системы в уста­новившемся режиме:

а при 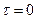выражение для корреляционной матрицы фазового век­тора

В частном случае, когда случайное воздействие u(t) —векторный белый шум с матрицей корреляционных функций , где — матрица интенсивностей шума,

ЧАСТОТНЫЙ МЕТОД

Данный метод используется в тех случаях, когда движе­ние летательного аппарата описывается системой линейных уравне­ний вида (2.1) с постоянными коэффициентами, а математические ожидания и дисперсии выходных координат вычисляются для ус­тановившегося режима, т. е. по окончании переходного процесса, обусловленного начальными условиями движения летательного ап­парата.

Переходная функция и частотная характеристика стационарной линейной системы. Пусть скалярное входное воздействие стацио­нарной устойчивой линейной системы u(t) — гармонический процесс 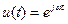, а в качестве выхода рассматривается одна из составляю­щих фазового вектора x(t). Если 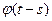- переходная функция, соответствующая рассматриваемым выходу x(t) и входу u(t), то в соответствии с (2.5) в стационарном режиме

Величину

являющуюся преобразованием Фурье от переходной функции , называют частотной характеристикой рассматриваемой линейной системы. Она характеризует реакцию системы по координате x(t) на гармоническое воздействие 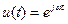. По известной передаточ­ной функции системы W(p), связывающей рассматриваемые вход и выход, частотную характеристику получают путем замены пере­менной р на 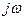, а сопряженную частотную характеристику W*( 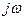) — на — .

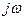Спектральная плотность выходной координаты. Пусть входное воздействие u(t) стационарной линейной системы — скалярный ста­ционарный процесс, а в качестве выходной переменной рассматри­вается составляющая x(t) фазового вектора в установившемся ре­жиме. В соответствии с (2.16) для, корреляционной функции ска­лярной переменной x(t) имеем

где — переходная функция, связывающая u(t) с x(t).

Корреляционная функция выходного процесса и его спектральная плотность связаны друг с другом преобразова­нием Фурье (1.56). Подстановка (2.21) в (1.56) дает

Учитывая, что

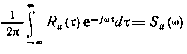
- спектральная плотность входного воздействия,

- частотная характеристика, связывающая u(t) с x(t),

- сопряженная частотная характеристика, получаем

Соотношение (2.23) устанавливает связь между спектральными плотностями входа и выхода стационарной линейной системы через ее частотную характеристику, если входное воздействие u(t) — ста­ционарный случайный процесс.

Дисперсия выходной координаты. Подстановка (2.23) в (1.56) позволяет найти корреляционную функцию выходной переменной

а в (1.57) —его дисперсию

Метод статистического анализа, основанный на использовании формулы (2.25) для определения дисперсии выходной координаты системы в установившемся режиме, называют частотным.

Математическое ожидание выходной переменной в установив­шемся режиме рассчитываем с помощью соотношения

где W_p — передаточная функция рассматриваемой системы, связы­вающая вход u(t) с выходом x(t).

Вычисление интеграла 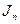. Если спектральная плотность — дробно-рациональная функция от , то вычисление дисперсии (2.25) может быть сведено к вычислению интеграла стандартного вида

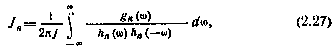
где

Все корни многочлена должны быть расположены в ле­вой полуплоскости. Значение интеграла (2.27) вычисляется по фор­муле [32]

где D_n — определитель Гурвица для полинома , вычисляемый на основе матрицы D_n с элементами

а определитель С_п вычисляется для матрицы С_п, получаемый из D_n путем замены ее первого столбца на b₀, b₁,..., b_n-1. Выражения для 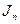при п= 1... 5 приведены в приложении 2.

Пример. Найдем дисперсию D_x переменной x(t) на выходе системы с пере­даточной функцией

и(р)

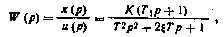
на вход которой поступает шум u(t) со спектральной плотностью . Имеем

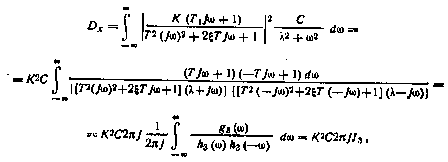
где

Здесь

В данном случае

Поэтому, учитывая, что b₀=0, получаем

Окончательно

ФОРМИРУЮЩИЕ ФИЛЬТРЫ

Формирующим фильтром называется динамическая си­стема или ее модель, реализованная на ЭВМ, свойства которой по­добраны так, что при подаче на вход системы белого шума 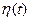на выходе получается случайный процесс x(t) с заданными статисти­ческими характеристиками. Задачу о построении формирующего фильтра приходится решать во всех случаях, когда статистический анализ системы, находящейся под воздействием небелых (окра­шенных) шумов, по тем или иным соображениям целесообразно за­менить анализом другой, расширенной системы, входные воздейст­вия которой — белые шумы. Как будет показано далее, подобная ситуация возникает, в частности, при статистическом анализе си­стем, возмущаемых окрашенными шумами, с использованием ме­тодов теории марковских процессов или метода статистического мо­делирования (Монте-Карло), а также при апостериорном оценива­нии состояния системы с помощью методов рекуррентной фильт­рации.

Очевидно, способ построения формирующего фильтра зависит от статистических характеристик рассматриваемого процесса x(t): скалярного или векторного, стационарного или нестационарного, гауссового или с произвольным распределением вероятностей. Для стационарного скалярного гауссовского случайного процесса фор­мирующий фильтр может быть построен с использованием соотно­шения (2.23). Действительно, как это следует из формулы (2.23), в тех случаях, когда спектральная плотность процесса x(t) может быть представлена в виде произведения комплексно сопря­женных сомножителей, один из которых есть частотная характери­стика искомого формирующего фильтра, а другой — его сопряженная частотная характеристика в качестве фор­мирующего фильтра может быть взята передаточная функция , соответствующая частотной характеристике .

Пример. Для случайного процесса x(t) со спектральной плотностью 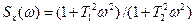формирующий фильтр имеет передаточную функ­цию

Поскольку для него

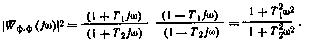
Если ввести вспомогательную переменную и рассматривать ее в качестве фазовой координаты фильтра, то передаточной функции (2.30) можно поставить в соответствие уравнение формирующего фильтра в нормаль­ной форме Коши относительно этой переменной:

где 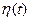—стандартный белый шум.

Интересующий нас процесс x(t) получаем из и 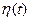с помощью соотношения .

спектральная плотность —не рациональная дробь, для определения формирующего фильтра с помощью соотношения (2.23) целесообразно провести аппроксимацию заданной функции дробно-рациональной функцией. Способы построения фор­мирующих фильтров для нестационарных гауссовских случайных процессов, а также для стационарных векторных корреляционных процессов рассмотрены в книге [24].