Определение состояния спускаемого аппарата по данным автономных измерений с использованием квазилинейного фильтра Калмана

Рассмотрим задачу навигации спускаемого аппарата (СА) с малым и средним аэродинамическим качеством по данным автономных измерений. Пусть информация, необходимая для ре­шения задачи навигации, поступает от датчиков перегрузок (аксе­лерометров), а для обработки информации используется бортовая цифровая вычислительная машина (БЦВМ). В качестве случайных возмущений, оказывающих влияние на процесс оценивания состоя­ния СА, рассматриваются начальные ошибки «входа» в атмосферу, разбросы аэродинамических характеристик, геометрических и кон­структивных параметров СА, порывы ветра, вариации плотности атмосферы, ошибки измерения перегрузок СА.

В соответствии с постановкой задачи байесовского оценивания необходимо записать стохастическое дифференциальное уравнение для расширенного вектора состояния, подлежащего оцениванию. В компоненты этого расширенного состояния, помимо переменных, характеризующих положение и скорость СА, включаются также указанные выше возмущения. Следовательно, для возмущений.должны быть записаны стохастические дифференциальные уравне­ния или уравнения формирующих фильтров.

Особую сложность представляет проблема построения форми­рующих фильтров для атмосферных возмущений — ветра и вариа­ций плотности,— поскольку в настоящее время эти возмущения при­нято рассматривать как нестационарные по высоте полета случай­ные процессы.

Остановимся на построении формирующих фильтров для атмо­сферных возмущений подробнее. Ветер принято задавать в виде трех статистически независимых составляющих, одна из которых горизонтальна и лежит в плоскости Z = 0, где Z — боковое от­клонение положения центра масс СА в скоростной системе коорди­нат, другая вертикальна и также лежит в плоскости Z = 0, а третья перпендикулярна плоскости Z = 0. Каждая из состав­ляющих скорости ветра W рассматривается как нестационарный гауссовский процесс, заданный в виде отрезка канонического разложений , где h — высота полета; , i—1, 2,...,

n - координатные функции; — случайные величины, такие, что , где — символ Кронекера. Приведенный отрезок ка­нонического разложения однозначно определяет корреляционную функцию составляющей скорости ветра:

Аналогично вариации плотности атмосферы 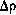рассматривают­ся как нестационарный по высоте случайный процесс и задаются в виде отрезка канонического разложения

— координатные функции. Это разложение определяет корреляционную функцию вариаций плотности:

Поскольку случайные процессы W и нестационарны по высоте, соответствующие формирующие фильтры для этих процессов также должны быть нестационарными.

Для того чтобы построить нестационарный формирующий фильтр, необходимо задать корреляционную функцию соответст­вующего случайного процесса в виде

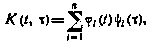
где — аргументы корреляционной функции, а последовательности образуют систему линейно независимых функций. При этом порядок уравнения формирующего фильтра равен числу членов канонического разложения я, которое может быть достаточ­но велико (n= 12...14).

С целью сокращения порядка формирующего фильтра может быть поставлена задача построения формирующего фильтра поряд­ка не выше заданного. Математически задача формируется следую­щим образом. Для нестационарного гауссовского процесса y(t) с корреляционной функцией K() требуется подобрать линейный дифференциальный оператор заранее заданного порядка, такой, чтобы корреляционная функция K*() случайного процесса x(t), полученного воздействием белого шума на фор­мирующий фильтр, определяемый L(p, t), как можно меньше отли­чалась бы от K() в смысле некоторого критерия.

Считаем, что корреляционная функция K() «гладко стекает» с диагонали квадрата — отрезок не­зависимой переменной, на котором задан процесс y(t). Иными сло­вами, предполагается, что скачки производных корреляционной функции K(t, x) по ее аргументам при t = отсутствуют. Это озна­чает, что в правой части дифференциального уравнения формирую­щего фильтра будут отсутствовать производные от белого шума [34] и задача сведется к определению коэффициентов следующего дифференциального уравнения формирую­щего фильтра:

Этому уравнению соответствует система из л-уравнений 1-го поряд­ка для n-мерного вектора х, включающего переменную и ее (п —1) производную:

Дифференциальное уравнение для корреляционной матрицы век­тора х (2.70) здесь имеет вид

где — интенсивность шума , или, в скалярной форме

В (3.101) K_ij — элементы корреляционной матрицы К_х. Посколь­ку матрица К_х и производные ее элементов считаются известны­ми на основании исходных статистических данных, систему уравнений (3.101) можно рассматривать как алгебраическую относительно не­известных . Нетрудно видеть, что из п² уравнений сис­темы (3.101) только п уравнений содержат коэффициенты — всего n+1 коэффициент. Таким образом, систе­ма уравнений (3.101) является неопределенной относительно и .

Выбор коэффициентов дифференциального уравнения форми­рующего фильтра будем осуществлять в процессе минимизации кри­терия J, характеризующего близость сечений поверхности заданной корреляционной функции и корреляционной функции случайного процесса на выходе формирующего фильтра.

В качестве критерия можно принять квадратичный: , причем сечения получить путем интегриро­вания уравнений

при начальных условиях

где —элементы корреляционной матрицы К_х в соответст­вующие моменты времени.

Заметим, что и, следовательно, критерий J не зависят b(t).

При заданном порядке формирующего фильтра количество на­чальных условий должно равняться порядку фильтра. Так, напри­мер, если ограничимся первым порядком, то обеспечим совпадение дисперсии случайного процесса на выходе формирующего фильтра с дисперсией заданного случайного процесса. При втором порядке формирующего фильтра, кроме совпадения дисперсий, будет совпа­дать и первая производная на диагонали квадрата заданной корреляционной функции с производной корре­ляционной функции на выходе формирующего фильтра. Если поря­док уравнения будет n, то будут совпадать дисперсия и (п —1) про­изводных сечений корреляционных функций и . Таким образом, определяем коэффициенты в результате ми­нимизации функционала . Минимизация осуществля­ется, например, методом наискорейшего спуска [28]. Коэффициент b(t) определяем из последнего уравнения системы (3.101).

Анализ корреляционных функций , по­лученных по экспериментальным данным, проведенный в [20], по­казывает, что разумным порядком формирующего фильтра для ветра и вариаций плотности атмосферы является второй, так что соответствующее возмущение характеризуется ее величиной и пер­вой производной по высоте полета: . Производные более высокого порядка вводить нецелесообразно, так как они не обладают достаточной достоверностью.

Таким образом, формирующий фильтр ветра определяется урав­нениями

Здесь — обратная высота; h₀ — начальная высота спус­ка; h — текущая высота полета.

Это означает, что уравнения формирующего фильтра (3.102) записаны по обратной высоте, поскольку движение СА происходит при убывании высоты, а поэтому корреляционная функция процесса на входе формирующего фильтра должна_ховпадать с исходной именно при убывании высоты h, т. е. при возрастании обратной вы­соты h_обр.

Аналогично записывается и определяется дифференциальное уравнение формирующего фильтра для Δр:

Возможен и иной подход к построению формирующих фильтров для атмосферных возмущений, основанный на использовании так называемых локальных моделей. Сущность этого подхода сводится к следующему.

При вычислении оценок текущего состояния динамической си­стемы точность статистического описания возмущений важна на том отрезке времени, где производится очередное измерение.

Поэтому возможно использование математических моделей ат­мосферных возмущений, дающих хорошее приближение лишь на малых отрезках . Такие модели, называемые в дальнейшем локальными, вообще говоря, различны для различных отрезков . Вид и способ задания локальных моделей определяется в каждом конкретном случае отдельно: это может быть отрезок канонического разложения малой размерности, формирующий фильтр первого порядка. Можно использовать на всем отрезке [0, Т] модель одного вида, периодически изменяя («настраивая») ее па­раметры. Для этого при переходе от отрезка к следующему в качестве априорных оценок параметров модели на отрезке необходимо принять апостериорные оценки этих парамет­ров, полученные на предыдущем интервале.

В качестве примера рассмотрим локальную модель вариаций плотности атмосферы. Для описания вариаций плотности в малом слое

будем основываться на простой экспоненциальной модели зависи­мости плотности от высоты:

где — значение плотности на некоторой фиксированной вы­соте —константа. Фактическая плотность p(h) будет отли­чаться от номинальной на :

где 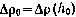— случайная величина; — случайное отклонение показателя экспоненты от номинального значения . Таким обра­зом, значение определяется двумя случайными величинами: .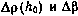

Введем величину :

Разлагая в ряд Тейлора по степеням с точностью до чле­нов первого порядка малости, получаем

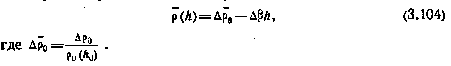
Выражение (3.104) представляет собой локальную параметри­ческую модель вариаций плотности воздуха. Если для величин записать формальные уравнения формирующих фильтров, то получим векторную форму локальной модели:

Кроме атмосферных возмущений, математические модели кото­рых приведены выше, необходимо учитывать разбросы аэродинами­ческих и конструктивных параметров СА: координат центра масс, площади миделя, аэродинамических коэффициентов. В каждой реа­лизации процесса спуска значения этих параметров не известны заранее и задаются своими априорными статистическими характе­ристиками так, что в целом для совокупности реализаций спуска они — величины случайные.

Будем полагать, что эти случайные величины статистически не­зависимы и подчиняются гауссовским законам распределения. Ана­логичный характер имеют и отклонения начальных условий «вхо­да».

Возмущения типа случайных параметров образуют вектор q, для которого можно записать формальное дифференциальное уравнение

с начальным условием q(0) (случайный вектор с характеристика­ми: — диагональная матрица).

Перейдем к построению модели оцениваемого процесса в целом. С целью упрощения рассмотрим движение СА в вертикальной плос­кости. При этом с целью дальнейшего упрощения уравнений дви­жения будем считать, что влияние ветра на движение СА сводится к изменению аэродинамических сил X и У и момента M_z только за счет изменения величины скорости и возникновения дополнитель­ного угла атаки согласно соотношениям

где Vw — воздушная скорость СА; У — скорость СА; — угол на­клона вектора скорости к местному горизонту; — приращение угла атаки; W — горизонтальная скорость ветра.

Вертикальная составляющая принимается равной нулю. Пред­полагается, что управление СА в вертикальной плоскости происхо­дит путем разворотов его по крену вокруг вектора скорости. При этом СА балансируется на некотором номинальном угле атаки. При изменении угла крена изменяется проекция нормальной силы на вертикальную плоскость, что позволяет управлять дальностью по­лета СА. Наличие углов крена разных знаков используется для парирования боковых отклонений СА. Управление углом крена осу­ществляется с помощью газореактивной системы. С учетом этих допущений уравнения движения СА в вертикальной плоскости в скоростной системе координат имеют вид [19]

В этих уравнениях введены следующие обозначения:

L — дальность, измеренная по дуге большого круга от точки входа в атмосферу до СА; - воздушный скоростной напор;

m — масса СА; R — радиус Земли, , — коэффициенты нормаль­ной и тангенциальной аэродинамических сил; s_M — площадь миделя; — угол крена, J_х — момент инерции СА относительно оси Ох; М_упр — управляющий момент по крену.

К системе (3.107) следует добавить уравнения формирующих фильтров для ветра и плотности воздуха (3.102) и (3.103) или, если используется локальная модель вариаций плотности, (3.105) вместо (3.103).

Однако в уравнениях формирующих фильтров (3.102), (3.103) и (3.105) независимой переменной является не время, а высота, вследствие чего эти уравнения не могут быть непосредственно ис­пользованы совместно с системой уравнений (3.107). Учитывая диф­ференциальную связь между временем и высотой dh/dt—Vsin , уравнения формирующих фильтров можно привести к виду

Здесь W — вектор 2×1, компонентами которого являются скорость ветра и ее производная по времени; — вектор 2×1, компонентами которого являются вариации плотности воздуха и ее производная по времени; A_w, , B_w, — матрицы 2×2 и 2×1 соответственно вида

— белые шумы.

Кроме уравнений (3.108), к системе (3.107) следует добавить дифференциальные уравнения (3.106) для возмущений, рассматри­ваемых как случайные величины. Вектор q для этих возмущений включает компоненты , где 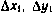— раз­бросы координат центра масс СА; — разброс площади миделя; — разбросы коэффициентов нормальной и тангенциальной аэродинамических сил. Сформируем расширенный вектор состояния х (15x1) СА с компонентами

где W, p, q — векторы соответствующих размерностей, определяе­мых формирующими фильтрами для этих возмущений.

Вектору х соответствует стохастическое дифференциальное уравнение

где f — вектор-функция, образованная правыми частями диффе­ренциальных уравнений (3.106), (3.107), (3.108); — вектор белых шумов с компонентами ; В — матрица 15×2, устроенная следующим образом

причем символом 0_ij обозначены нулевые блоки соответствующих размерностей; и — управляющее воздействие;

В качестве модели измерений рассмотрим соотношения

т. е. будем считать, что измерению доступны перегрузки СА по свя­занным осям. Кроме того, будем полагать, что в нашем распоряжении имеется дополнительная информация относительно углов тан­гажа и крена, полученная с помощью соответствующих гироскопов, установленных на борту СА. С целью упрощения модели измерений, а также вследствие относительно малого времени спуска считаем, что систематические ошибки измерений отсутствуют и измерения, осуществляемые дискретно, сопровождаются ошибками, представ­ляющими собой дискретную последовательность статистически не­зависимых гауссовских случайных величин , таких, что , — диагональная матрица l×l (l — размерность век­тора измерений ). Таким образом, модель измерений имеет вид

причем формируется на основе оценок вектора . Для обра­ботки информации целесообразно использовать квазилинейный фильтр Калмана, описываемый соотношениями (3.95), (3.96), (3.98), (3.99).

Эффективность алгоритма, описываемого этими соотношениями, может быть проверена имитационным моделированием процесса навигации гипотетического СА, для которого разброс геометриче­ских и конструктивных параметров характеризуется относительным средним квадратичным отклонением в 2%. Ошибки «входа» можно считать соответствующими следующим среднеквадратичным от­клонениям:

Ошибки измерения ускорений примем соответствующими среднему квадратичному отклонению 2-10^-3 м/с²; ошибки измерения угловых величин — средним квадратичным отклонениям 0,01°.

При использовании модифицированного квазилинейного фильт­ра Калмана в данной задаче необходимо учитывать следующее. Формальное применение такого алгоритма может привести к рез­кому увеличению объема вычислений по сравнению с линейным фильтром Калмана и, как следствие, к повышенным требованиям к объему памяти, длине разрядной сетки и быстродействию БЦВМ. Поэтому можно предложить следующую последовательность дейст­вий при построении оценок компонент вектора состояния СА. Счи­тая все компоненты вектора состояния СА, кроме компонент и характеризующих угловое положение СА относительно цент­ра масс, известными, оцениваем последние, используя информацию от гироскопических датчиков. Получив эти оценки с некоторой точ­ностью, переходим к оцениванию компонент, характеризующих по­ложение и скорость центра масс, а также возмущающие воздейст­вия, полагая известными компоненты, характеризующие угловое положение СА. При этом интервал дискретности при оценке ком­понент углового положения СА относительно центра масс должен быть существенно (примерно на порядок) меньше, чем при оценке остальных компонент вектора х.

Такой подход вполне возможен, так как СА оснащен, как пра­вило, системой стабилизации углового движения, и переходные процессы по компонентам вектора состояния, характеризующим угловое положение СА, протека­ют быстрее, чем по компонентам, характеризующим положение и ско­рость центра масс СА. Следует указать также, что точность оценки уг­ла траектории сущест­венно зависит от точности оценки возмущений: ветра, вариаций плотности и разброса аэродинамических коэффициентов.

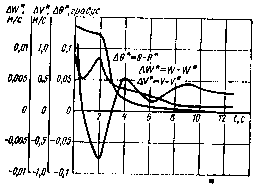
Поэтому целесообразно вначале проводить оценку составляю­щих возмущений при априорных значениях угла наклона траекто­рии, и только после уточнения возмущений переходить к совместной оценке компонент вектора х. Характер переходных процессов, воз­никающих при таком способе оценивания в квазилинейном фильтре Калмана, показан на рис. 3.9. Апостериорные дисперсии компонент, характеризующих положение и скорость центра масс, а также воз­мущения приведены на рис. 3.10.

Рис. 3.10. Апостериорные дисперсии компонент вектора состояния ЛА