Естественным развитием квазилинейного фильтра Калма-на, основанного на линеаризации уравнений движения и соотношений для измерений в окрестности оптимальной оценки, полученной на предыдущем шаге измерений, является алгоритм, обеспечивающий дальнейший более полный учет нелинейных свойств соотношений для измерений. Такой учет может быть осуществлен аппроксимацией зависимостей, связывающих компоненты вектора состояния и вектора измерений, полиномами наилучшего в среднеквадратичном смысле приближения или полиномами с узлами, определяемыми оценкой, полученной на предыдущем шаге оценивания. Рассмотрим подробнее последний способ аппроксимации. Пусть модели изменения состояния и измерений совпадают с (3.90) и (3.91) соответственно. Представим компоненты  вектор-функции gi, входящей в выражение (3.91), в виде
вектор-функции gi, входящей в выражение (3.91), в виде

где  — вектор состояния и его компоненты;
— вектор состояния и его компоненты;  —прогнозированная оценка компоненты
—прогнозированная оценка компоненты  , т. е. оценка этой компоненты, полученная по измерениям до момента
, т. е. оценка этой компоненты, полученная по измерениям до момента  включительно;
включительно;  —постоянные для данного момента коэффициенты.
—постоянные для данного момента коэффициенты.
|
|
|
Опишем способ определения этих коэффициентов. Обозначим

где  — диагональные элементы апостериорной корреляционной матрицы
— диагональные элементы апостериорной корреляционной матрицы  , характеризующие точность прогнозированных оценок
, характеризующие точность прогнозированных оценок 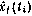 . Потребуем совпадения полинома и исходной нелинейной функции
. Потребуем совпадения полинома и исходной нелинейной функции  в момент
в момент  в четырех точках:
в четырех точках:

где  — матрицы 4×4, диагональные элементы j -й и r -й строк которых единицы, а остальные — нули.
— матрицы 4×4, диагональные элементы j -й и r -й строк которых единицы, а остальные — нули.
Из условия совпадения функций  в точках
в точках 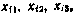 ,
,  найдем коэффициенты полинома:
найдем коэффициенты полинома:


Как и при использовании квазилинейного фильтра Калмана, по мере уточнения оценок компонент вектора состояния размеры области аппроксимации функции  полиномом
полиномом  уменьшаются. Заметим также, что в общем случае аппроксимация функции
уменьшаются. Заметим также, что в общем случае аппроксимация функции  может быть осуществлена полиномом, порядок которого выше второго. Однако при этом объем вычислений на каждом шаге измерений существенно увеличивается.
может быть осуществлена полиномом, порядок которого выше второго. Однако при этом объем вычислений на каждом шаге измерений существенно увеличивается.
В отдельных случаях точность оценивания может быть повышена путем использования для аппроксимации полинома наилучшего в среднеквадратичном смысле приближения.
С целью получения соотношений, удобных для реализации на ЭВМ, введем в момент ti,(i — 0, 1, 2,..., N) расширенный вектор фазовых координат  в виде
в виде

Иначе говоря, будем вводить компоненты вектор-функции 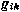 поочередно в пределах одного шага измерений ti в число компонент расширенного вектора состояния оцениваемой динамической системы. В результате окажется, что одна из компонент расширенного вектора состояния, а именно
поочередно в пределах одного шага измерений ti в число компонент расширенного вектора состояния оцениваемой динамической системы. В результате окажется, что одна из компонент расширенного вектора состояния, а именно  , измеряется непосредственно. При этом компоненты вектора измерений yi, относящиеся к моменту ti, будут обрабатываться поочередно; апостериорные характеристики компонент вектора состояния, полученные в результате обработки
, измеряется непосредственно. При этом компоненты вектора измерений yi, относящиеся к моменту ti, будут обрабатываться поочередно; апостериорные характеристики компонент вектора состояния, полученные в результате обработки  -й компоненты вектора
-й компоненты вектора  , будут априорными при обработке (k+1)-й компоненты вектора yi и т. д.
, будут априорными при обработке (k+1)-й компоненты вектора yi и т. д.
|
|
|
С введением вектора  возникает необходимость в определении статистических характеристик этого вектора, априорных по отношению к обрабатываемому измерению. Здесь ограничимся определением априорных математического ожидания и корреляционной матрицы вектора
возникает необходимость в определении статистических характеристик этого вектора, априорных по отношению к обрабатываемому измерению. Здесь ограничимся определением априорных математического ожидания и корреляционной матрицы вектора  т. е. характеристик не выше второго порядка.
т. е. характеристик не выше второго порядка.
Для того чтобы найти математическое ожидание вектора  , достаточно определить априорное математическое ожидание его компоненты
, достаточно определить априорное математическое ожидание его компоненты 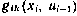 . В соответствии с выражением (3.113) имеем
. В соответствии с выражением (3.113) имеем


Априорная корреляционная матрица вектора  определяется в виде
определяется в виде
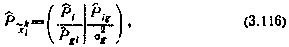
где  — априорная дисперсия компоненты
— априорная дисперсия компоненты  ;
;  — матрица взаимных корреляционных моментов компонент вектора состояния
— матрица взаимных корреляционных моментов компонент вектора состояния  ; и компоненты
; и компоненты  . В соответствии с выражением (3.113), полагая третьи моменты равными нулю, определяем
. В соответствии с выражением (3.113), полагая третьи моменты равными нулю, определяем

где  — центральные моменты четвертого порядка, выражаемые через центральные моменты второго порядка следующим образом [34]:
— центральные моменты четвертого порядка, выражаемые через центральные моменты второго порядка следующим образом [34]:
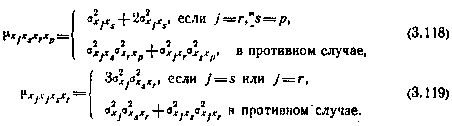
Взаимные корреляционные моменты компонент  и
и  , j— 1, 2,..., п, определяющие элементы матриц
, j— 1, 2,..., п, определяющие элементы матриц  всоответствии с (3.113), могут быть записаны при условии, что третьи моменты равны нулю, в виде
всоответствии с (3.113), могут быть записаны при условии, что третьи моменты равны нулю, в виде

где 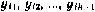 — компоненты вектора
— компоненты вектора  .
.
Таким образом, с помощью приведенных выше соотношений (3.115), (3.117), (3.118), (3.119) статистические характеристики вектора  определяющие его априорную к моменту обработки k-й составляющей вектора уi плотность вероятностей как гауссовскую, определены.
определяющие его априорную к моменту обработки k-й составляющей вектора уi плотность вероятностей как гауссовскую, определены.
Для определения апостериорных характеристик вектора  можно формально применить соотношения (3.42), (3.43), определяющие линейный дискретный фильтр Калмана, с учетом того, что при принятой схеме обработки матрица H, связывающая k-ю (k = 1, 2,..., l) компоненту вектора уi с компонентами вектора
можно формально применить соотношения (3.42), (3.43), определяющие линейный дискретный фильтр Калмана, с учетом того, что при принятой схеме обработки матрица H, связывающая k-ю (k = 1, 2,..., l) компоненту вектора уi с компонентами вектора  представляет собой матрицу-строку 1× (n×1), первые n-столбцов которой нули, а последний — единица:
представляет собой матрицу-строку 1× (n×1), первые n-столбцов которой нули, а последний — единица:

где 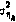 — дисперсия ошибки измерения k-й компоненты вектора уi, yik — значение k-й компоненты вектора уi,
— дисперсия ошибки измерения k-й компоненты вектора уi, yik — значение k-й компоненты вектора уi,  — апостериорная ковариационная матрица вектора
— апостериорная ковариационная матрица вектора  , т. е. матрица, получающаяся после обработки k-й компоненты вектора уi,
, т. е. матрица, получающаяся после обработки k-й компоненты вектора уi,  — байесовская оценка вектора
— байесовская оценка вектора 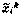 , полученная в результате обработки k-й компоненты вектора уi.
, полученная в результате обработки k-й компоненты вектора уi.
Так как обрабатываемые измерения являются скалярными, то соотношения фильтра второго порядка удобно записать в скалярной форме:

В этих соотношениях  - соответственно элементы априорной и апостериорной ковариационных матриц, полученные до и после обработки компоненты
- соответственно элементы априорной и апостериорной ковариационных матриц, полученные до и после обработки компоненты 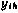 вектора
вектора  — соответственно априорная и апостериорная оценки компонент вектора
— соответственно априорная и апостериорная оценки компонент вектора 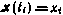 при тех же условиях.
при тех же условиях.
«Начальные условия» для рекуррентных соотношений, описывающих фильтр второ-го порядка, те же, что и для описанных выше байесовских алгоритмов. Переход от момента 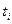 к моменту
к моменту  в фильтре второго порядка происходит также, как и в квазилинейном фильтре Калмана, т. е. с помощью соотношений (3.95), (3.96).
в фильтре второго порядка происходит также, как и в квазилинейном фильтре Калмана, т. е. с помощью соотношений (3.95), (3.96).
 2015-10-22
2015-10-22 507
507








