Применение принципа минимума для программирования оптимального управления проиллюстрируем сначала на следующем примере.
Пусть в бессиловом поле движется летательный аппарат под действием силы тяги двигателя. Математическая модель такого аппарата может быть упрощенно представлена в виде уравнений движения
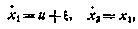
где  — скорость аппарата;
— скорость аппарата; 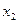 — путь, пройденный к текущему моменту времени; и — программная, неслучайная составляющая управляющего ускорения;
— путь, пройденный к текущему моменту времени; и — программная, неслучайная составляющая управляющего ускорения;  — случайное возмущение программной составляющей. Полагаем, что статистические характеристики возмущения
— случайное возмущение программной составляющей. Полагаем, что статистические характеристики возмущения  известны, причем
известны, причем 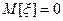 . Для простоты считаем также, что ограничения на управление отсутствуют. Поставим задачу определения такой программы u(t), которая обеспечила бы перевод летательного аппарата из заданного начального состояния
. Для простоты считаем также, что ограничения на управление отсутствуют. Поставим задачу определения такой программы u(t), которая обеспечила бы перевод летательного аппарата из заданного начального состояния 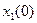 ,
,  в желаемое конечное состояние
в желаемое конечное состояние 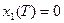 ,
, 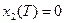 с минимальным значением критерия
с минимальным значением критерия
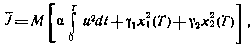
где 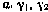 — заданные числа.
— заданные числа.
Интегральное слагаемое в этом критерии характеризует среднее значение расхода топлива, затрачиваемого на процесс управления, а величина  является мерой близости конечного состояния к желаемому. Коэффициент а показывает весовую долю этих составляющих в общем критерии оптимальности.
является мерой близости конечного состояния к желаемому. Коэффициент а показывает весовую долю этих составляющих в общем критерии оптимальности.
Для решения данной задачи воспользуемся необходимыми условиями оптимальности (4.45) с учетом (4.49), (4.47), (4.44). Согласно этим соотношениям гамильтониан Н будет равен
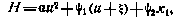
где компоненты сопряженного вектора определяются согласно уравнениям
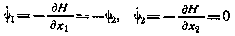
с граничными условиями

а само условие достижения гамильтонианом минимального по управлению значения примет вид
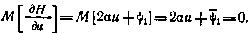
Отсюда искомое управление следующим образом связано с сопряженной переменной  :
:

Из сопряженной системы уравнений находим

Поэтому
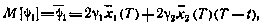
и оптимальное управление равно
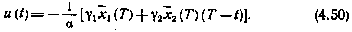
В свою очередь согласно исходным уравнениям движения математические ожидания  и
и 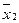 удовлетворяют уравнениям
удовлетворяют уравнениям
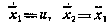
при начальных условиях 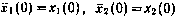 . Интегрируя эту систему с учетом найденного управления, получаем
. Интегрируя эту систему с учетом найденного управления, получаем
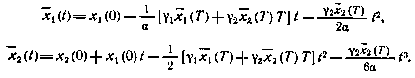
Полагая здесь t = T, получаем линейную систему алгебраических уравнений относительно неизвестных величин х i (T), х2(Т). Таким образом, в данном примере краевая задача свелась к системе линейных алгебраических уравнений второго порядка относительно  (Т),
(Т), 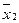 (Т). Определяя их, т. е. решая указанную систему и подставляя решение в выражение (4.50), окончательно получаем искомую программу управления.
(Т). Определяя их, т. е. решая указанную систему и подставляя решение в выражение (4.50), окончательно получаем искомую программу управления.
А теперь рассмотрим задачу управления линейной системой более общего вида:

где А, В — матрицы, зависящие в общем случае от времени;  — случайное возмущение типа «белого шума» с нулевым математическим ожиданием
— случайное возмущение типа «белого шума» с нулевым математическим ожиданием
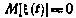
и корреляционной функцией
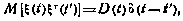
где 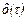 -
- 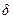 -функция; D(t) -матрица интенсивностей белого шума.
-функция; D(t) -матрица интенсивностей белого шума.
Поставим задачу определения такой матрицы коэффициентов обратной связи L(t) в зависимости

которая обеспечила бы минимизацию интегротерминального критерия

Предполагается, что матрицы W,  положительно определены. Статистические характеристики вектора начального состояния х(0) считаются известными.
положительно определены. Статистические характеристики вектора начального состояния х(0) считаются известными.
Отметим, что сформулированная задача является также задачей программирования оптимального управления. Правда, в качестве искомого управляющего воздействия теперь является зависимость матрицы L от времени.
Составим гамильтониан для данной задачи. Так как с учетом (4.52) система (4.51) и критерий оптимальности могут быть представлены в виде

то согласно (4.49)

При оптимальном управлении (в данном случае при оптимальной матрице L) сопряженный вектор 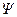 согласно (4.47) удовлетворяет уравнению:
согласно (4.47) удовлетворяет уравнению:
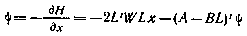
с граничным условием (4.44)

Ввиду отсутствия ограничений на управление необходимые условия оптимальности (4.45) принимают вид
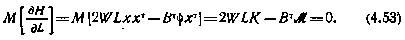
Здесь для краткости введены обозначения
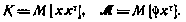
Нетрудно установить, что матрица К удовлетворяет следующему дифференциальному уравнению:
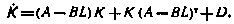
С целью определения второй ковариационной матрицы M установим сначала связь векторов 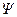 и х для произвольного момента t. Запишем уравнения, определяющие эти векторы, в виде системы
и х для произвольного момента t. Запишем уравнения, определяющие эти векторы, в виде системы
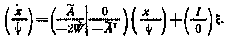
Здесь для краткости даны следующие обозначения:  — единичная матрица.
— единичная матрица.
Пусть  —фундаментальная матрица этой системы, т. е. матрица, удовлетворяющая уравнению
—фундаментальная матрица этой системы, т. е. матрица, удовлетворяющая уравнению
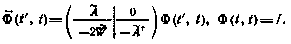
Тогда общее решение для х и 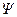 можно представить так:
можно представить так:
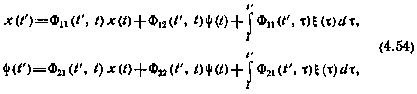
где  — соответствующие блоки матрицы Ф. Нетрудно заметить, что в данном случае блок
— соответствующие блоки матрицы Ф. Нетрудно заметить, что в данном случае блок 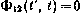 для любых моментов t. Другими словами, решение для вектора х не зависит от вектора
для любых моментов t. Другими словами, решение для вектора х не зависит от вектора 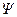 .
.
С учетом найденных решений (4.54) связь между векторами х и 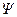 для конечного момента Т принимает вид
для конечного момента Т принимает вид
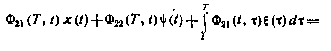

Отсюда полагая, что матрица Ф22(T,t) неособенная, получаем связь 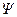 и х для любого момента времени:
и х для любого момента времени:

где
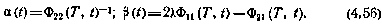
Перемножая  и
и 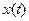 и производя операцию математического ожидания, получаем
и производя операцию математического ожидания, получаем

В силу свойств 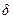 -функции интегральный член в этом выражении равен нулю. Поэтому матрицу M можно представить в виде
-функции интегральный член в этом выражении равен нулю. Поэтому матрицу M можно представить в виде

где

Таким образом, матрица ковариации векторов 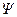 и х линейно связана с матрицей вторых моментов К в любой момент времени.
и х линейно связана с матрицей вторых моментов К в любой момент времени.
Подчеркнем теперь, что как матрица 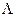 , так и матрица К не зависят от значений матрицы L в текущий момент t. Правда, матрица
, так и матрица К не зависят от значений матрицы L в текущий момент t. Правда, матрица 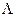 зависит через элементы матрицы
зависит через элементы матрицы 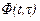 от всех значений
от всех значений 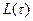 при
при  , а матрица К — от значений
, а матрица К — от значений 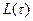 при
при  . Учитывая это, из условия (4.53) можно записать следующее выражение для оптимального значения матрицы L в текущий момент времени:
. Учитывая это, из условия (4.53) можно записать следующее выражение для оптимального значения матрицы L в текущий момент времени:

Чтобы воспользоваться этим соотношением, необходимо определить матрицу Л. Формально она определяется в соответствии с соотношениями (4.56), (4.55). Однако нетрудно получить и уравнение, определяющее матрицу 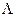 непосредственно. Для этого продифференцируем соотношение (4.57). С учетом уравнения для матрицы К получим
непосредственно. Для этого продифференцируем соотношение (4.57). С учетом уравнения для матрицы К получим

С другой стороны, на основе определения матрицы M учетом уравнений для векторов х и 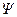 имеем
имеем
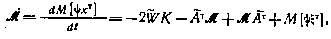
причем согласно (4.54) и (4.55)
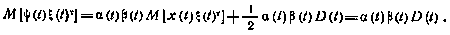
Объединяя эти уравнения, получаем

Это уравнение выполняется тождественно при любых матрицах К, если 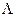 удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению

Раскрывая здесь смысл матриц  ,
,  и принимая во внимание выражение (4.58), окончательно получаем
и принимая во внимание выражение (4.58), окончательно получаем
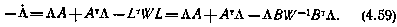
Граничное условие для этого матричного уравнения получается из сравнения выражения (4.57) для момента

и аналогичного соотношения для Ж{Т) согласно определению

Поэтому

Таким образом, задача определения оптимальных коэффициентов обратной связи в линейном законе управления сводится к решению обыкновенного матричного дифференциального уравнения (4.59) при граничном условии (4.60).
ЗАДАЧА ОПТИМАЛЬНОГО ПЛАНИРОВАНИЯ НАВИГАЦИОННЫХ ИЗМЕРЕНИЙ
Задачу оптимального планирования навигационных измерений будем интерпретировать как задачу отыскания оптимальной программы управления некоей фиктивной динамической системой, в качестве которой рассмотрим алгоритм оценивания, в простейшем случае — линейный фильтр Калмана. Кроме того, в отличие от предыдущего раздела с целью получения более наглядных результатов задачу обработки информации рассмотрим в непрерывной постановке.
Итак, пусть имеется линейная динамическая система

состояние которой x(t) требуется оценить. В (4.61) x(t) —вектор n×1; A(t) —матрица п × п;  —вектор белых шумов с матрицей
—вектор белых шумов с матрицей
интенсивностей  . Модель (4.61) идентична модели (3.49) при
. Модель (4.61) идентична модели (3.49) при 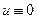 .
.
Будем считать, что на интервале (t0, T) измеряются m векторных процессов размерности l m×1 каждый, причем уравнения измерителей однотипны и имеют вид
где Hk — матрица l k×n; 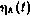 —вектор белого шума размерности
—вектор белого шума размерности  с матрицей интенсивностей
с матрицей интенсивностей 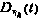 .
.
Точность оценивания состояния х(t) системы (4.61) по измерениям (4.62), как и в разд. 3.6.1, определяется с помощью апостериорной корреляционной матрицы P*(t), изменение которой в силу непрерывности измерений, описывается уравнением, аналогичным (3.57):

Уравнение (4.63) отличается от (3.57) наличием суммы в правой части. Эта сумма обусловлена тем, что измеряется не один, а т векторных процессов  . Будем рассматривать (4.63) как некоторую управляемую динамическую систему, в которой т — мерный вектор управления u(t) с компонентами
. Будем рассматривать (4.63) как некоторую управляемую динамическую систему, в которой т — мерный вектор управления u(t) с компонентами 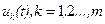 , задает программу измерений векторов
, задает программу измерений векторов 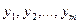 .В дальнейшем будем считать, что компоненты
.В дальнейшем будем считать, что компоненты  вектора и принадлежат множеству U, состоящему из двух элементов 0 и
вектора и принадлежат множеству U, состоящему из двух элементов 0 и  :
:

где

В (4.65) под  будем понимать множество моментов времени, в которые можно (по техническим причинам) проводить измерения процессов
будем понимать множество моментов времени, в которые можно (по техническим причинам) проводить измерения процессов  . С учетом (4.64), (4.65) программа u(t) имеет наглядный физический смысл: если
. С учетом (4.64), (4.65) программа u(t) имеет наглядный физический смысл: если 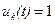 , то в момент t k-e измерительное средство используется, если
, то в момент t k-e измерительное средство используется, если  — не используется.
— не используется.
В том случае, если в конкретной технической задаче два различных измерителя не могут работать одновременно, то на компоненты вектора и накладывается дополнительное ограничение

В конкретной технической задаче планирования эксперимента по уточнению состояния динамической системы наиболее распространенной является ситуация, когда необходимо выполнить требования по точности оценки какого-либо скалярного параметра, характеризующего движение летательного аппарата, при ограничении на время наблюдения в силу условий видимости, загруженности командно-измерительного или бортового навигационного комплекса и т. д.
Поэтому представляет интерес следующая задача. Требуется определить вектор u*(t), минимизирующий критерий
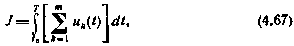
характеризующий временные затраты на измерения при ограничении на конечную точность оценивания скалярного параметра s = аТх(Т), характеризуемую апостериорной дисперсией  . Сформулированную задачу будем рассматривать как задачу программирования оптимального управления в системе (4.63) по критерию (4.67) при ограничениях на управление (4.64) — (4.65) и на конечное состояние
. Сформулированную задачу будем рассматривать как задачу программирования оптимального управления в системе (4.63) по критерию (4.67) при ограничениях на управление (4.64) — (4.65) и на конечное состояние 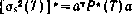 . Непосредственное решение подобной задачи [36] приводит к необходимости решения краевой задачи, размерность которой определяется числом различных элементов матрицы Р* в (4.63), т. е.
. Непосредственное решение подобной задачи [36] приводит к необходимости решения краевой задачи, размерность которой определяется числом различных элементов матрицы Р* в (4.63), т. е. 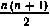 , и сопряжено со
, и сопряжено со
значительными трудностями. С целью их преодоления воспользуемся следующим приемом. Введем некоторые п- мерные векторы 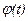 , q(t) таким образом, чтобы во все моменты времени на интервале (t0, T) выполнялось тождество
, q(t) таким образом, чтобы во все моменты времени на интервале (t0, T) выполнялось тождество

Дифференцируя левую и правую части соотношения (4.68) с учетом (4.63) и требуя выполнения получающегося равенства при любых P*(t), получаем систему дифференциальных уравнений для 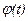 и q(t).
и q(t).
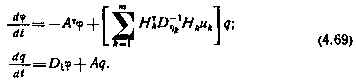
Действительно,
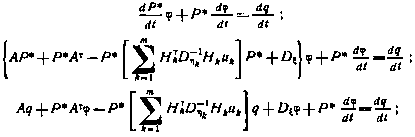
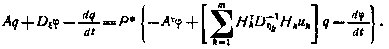
Из последнего выражения непосредственно следует (4.69). В силу (4.68) на начальные условия этой системы уравнений наложены следующие ограничения:

Можно доказать, что если в системе (4.69) к ограничениям (4.70) добавить следующие ограничения на векторы  и q в момент Т:
и q в момент Т:
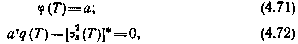
то задача программирования оптимального управления, задаваемая соотношениями (4.69) — (4.72), (4.64) — (4.67), будет эквивалентна исходной оптимизационной задаче в смысле управления u*(t).
Наиболее простое решение эквивалентной задачи получается при малой интенсивности шумов в модели (4.61), так что можно положить 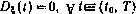 .
.
В этом случае система уравнений (4.69) принимает следующий вид:
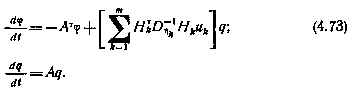
Рассмотрим последние п уравнений

Если  — фундаментальная матрица системы (4.74), то
— фундаментальная матрица системы (4.74), то

Умножим (4.75) слева на а т и с учетом (4.70), (4.72) получим

Таким образом, ограничение (4.72) сводится к ограничению на левом конце траектории:
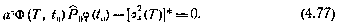
Обозначим
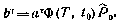
Тогда

При этом, поскольку решение системы (4.74) записано в явном виде (4.75), последнюю систему уравнений можно исключить из (4.73), так как 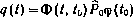 . Тогда
. Тогда
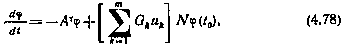
где
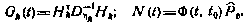
В результате проведенных преобразований система (4.73), имеющая размерность 2n, сведена к системе (4.78) размерности п. Теперь рассмотрим задачу программирования оптимального управления уже в системе (4.78) при ограничениях (4.64), (4.65), (4.71), (4.77) и критерии (4.67). В соответствии с приведенными условиями оптимальности составляем гамильтониан

Структуру оптимального управления 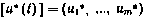 определим из условия максимума гамильтониана по u(t):
определим из условия максимума гамильтониана по u(t):

где 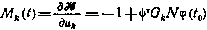 — программная функция.
— программная функция.
Система уравнений для n -мерного вектора сопряженных переменных 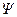 линейна:
линейна: 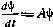 , и ее решение может быть записано на основе фундаментальной матрицы исходной системы (4.61):
, и ее решение может быть записано на основе фундаментальной матрицы исходной системы (4.61):

Начальные условия для вектора 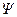 определяются с учетом (4.77) из условия трансверсальности:
определяются с учетом (4.77) из условия трансверсальности:

где x — постоянный множитель.
Подставим (4.81) в выражение для Mk(t) и, учитывая соотношение (4.82) для значения 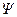 момент t 0, получим при k=1, 2,..., m следующее выражение:
момент t 0, получим при k=1, 2,..., m следующее выражение:
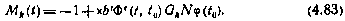
Получим краевую задачу для системы уравнений (4.78) при управлении (4.80), заключающуюся в подборе (п+ 1)-мерного вектора 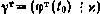 таким образом, чтобы выполнялись ограничения (4.71), (4.77). Последнее эквивалентно определению вектора
таким образом, чтобы выполнялись ограничения (4.71), (4.77). Последнее эквивалентно определению вектора  из решения следующей системы трансцендентных уравнений размерности (п+ 1):
из решения следующей системы трансцендентных уравнений размерности (п+ 1):
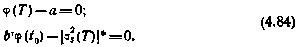
Для установления функциональной зависимости вектора конечного состояния 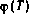 от вектора
от вектора 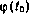 и скаляра x необходимо записать в явном виде решение системы (4.78) на основе формулы Коши. В результате получим
и скаляра x необходимо записать в явном виде решение системы (4.78) на основе формулы Коши. В результате получим
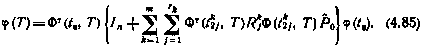
Здесь
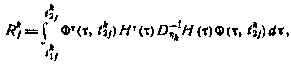
где 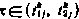 . Моменты времени
. Моменты времени 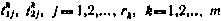 , являющаяся соответственно началом и концом мерных интервалов, количество которых равно
, являющаяся соответственно началом и концом мерных интервалов, количество которых равно  для k-го измерительного средства, определяются как корни уравнений
для k-го измерительного средства, определяются как корни уравнений
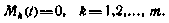
Для получения эффективной численной процедуры решения системы уравнений (4.84) преобразуем эту систему к более удобному для вычислений виду, разработав, кроме того, специальный прием определения начального приближения для вектора 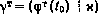 . Разрешим первые п уравнений системы (4.84) относительно ср(/0) на основе установленной ранее зависимости (4.85):
. Разрешим первые п уравнений системы (4.84) относительно ср(/0) на основе установленной ранее зависимости (4.85):

Моменты времени 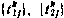 , зависящие в свою очередь от
, зависящие в свою очередь от 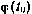 , будем искать как точки переключения программы u(t), определяемой соотношениями (4.80), (4.83). При этом множитель к в (4.83) подбираем из условия
, будем искать как точки переключения программы u(t), определяемой соотношениями (4.80), (4.83). При этом множитель к в (4.83) подбираем из условия 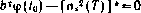 , тем самым решая последнее скалярное уравнение системы (4.84). Отметим, что в этом уравнении зависимость от к проявляется неявно через соотношения (4.80), (4.83). Очевидно, что с учетом сказанного решение системы (4.84) может быть сведено к отысканию корня
, тем самым решая последнее скалярное уравнение системы (4.84). Отметим, что в этом уравнении зависимость от к проявляется неявно через соотношения (4.80), (4.83). Очевидно, что с учетом сказанного решение системы (4.84) может быть сведено к отысканию корня 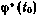 уравнения
уравнения
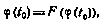
где под F понимается некоторый нелинейный оператор, определяемый (4.86) с учетом (4.80), (4.83). Для решения этого уравнения можно предложить метод последовательных приближений, приводящий к следующей итерационной процедуре:
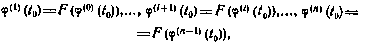
где 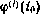 — i -e приближение,
— i -e приближение,  .
.
В процессе численного решения уравнения 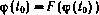 существенное значение имеет выбор достаточно хорошего начального приближения
существенное значение имеет выбор достаточно хорошего начального приближения 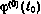 . Прием, используемый для его нахождения, состоит в приближенном решении задачи планирования на основе ее упрощения за счет замены критерия (4.67) квадратичным критерием
. Прием, используемый для его нахождения, состоит в приближенном решении задачи планирования на основе ее упрощения за счет замены критерия (4.67) квадратичным критерием 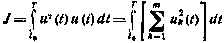 соответственно за счет снятия ограничений (4.64), (4.66). Последовательность решения упрощенной задачи управления системой (4.69) совпадает с рассмотренным ранее решением точной задачи, но из-за различия критериев приводит к несколько иным результатам. Можно показать, что в этом случае краевая задача, соответствующая квадратическому критерию, сводится к решению системы (n+1) алгебраических уравнений 2-го порядка. Решение этой системы можно получить, например, методом Ньютона.
соответственно за счет снятия ограничений (4.64), (4.66). Последовательность решения упрощенной задачи управления системой (4.69) совпадает с рассмотренным ранее решением точной задачи, но из-за различия критериев приводит к несколько иным результатам. Можно показать, что в этом случае краевая задача, соответствующая квадратическому критерию, сводится к решению системы (n+1) алгебраических уравнений 2-го порядка. Решение этой системы можно получить, например, методом Ньютона.
Для иллюстрации эффективности предложенного выше метода рассмотрим оптимальное планирование измерений в задаче определения состояния ИСЗ, движущегося по наклонной орбите, близкой к круговой. В качестве модели движения примем линейную систему уравнений, описывающую движение ИСЗ в окрестности опорной круговой орбиты:

где шестимерный вектор состояния Δх определяет отклонение ИСЗ от опорной орбиты в орбитальной подвижной системе координат, введенной в разд. 3.3.4 (см. рис. 3.22).
Введем вектор состояния ИСЗ с компонентами 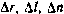 , где Δr — отклонение ИСЗ от положения на опорной орбите в направлении радиус-вектора; Δl — вдоль орбиты; Δn — по нормали к плоскости орбиты:
, где Δr — отклонение ИСЗ от положения на опорной орбите в направлении радиус-вектора; Δl — вдоль орбиты; Δn — по нормали к плоскости орбиты:
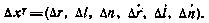
Воспользовавшись приемом, описанным в разд. 3.3.4, получим фундаментальную матрицу системы (4.87), формально совпадающую с (3.78) с точностью до постоянного множителя 1/r0 в диагональных элементах. В качестве измеряемого (навигационного) параметра рассмотрим суммарную наклонную дальность до ИСЗ —  . Пусть измерения проводятся двумя наземными измерительными пунктами на интервале (t0, T) с максимально допустимой частотой
. Пусть измерения проводятся двумя наземными измерительными пунктами на интервале (t0, T) с максимально допустимой частотой 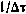 , где
, где 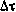 — шаг измерений. Быстро меняющиеся ошибки измерений представляют собой последовательность некоррелированных гауссовских величин
— шаг измерений. Быстро меняющиеся ошибки измерений представляют собой последовательность некоррелированных гауссовских величин 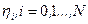 с характеристиками
с характеристиками  .
.
Предположим, что большая частота измерений позволяет перейти к непрерывной модели наблюдения. Тогда для каждого НИПа имеем

где 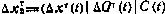 — расширенный вектор состояния, включающий компоненты;
— расширенный вектор состояния, включающий компоненты;  —отклонения гринвичских координат НИПа от расчетных значений; С(t) —систематическая (медленно меняющаяся) ошибка измерения
—отклонения гринвичских координат НИПа от расчетных значений; С(t) —систематическая (медленно меняющаяся) ошибка измерения  ;
; 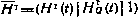 — блочная матрица, блок
— блочная матрица, блок 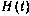 которой — матрица частных производных от суммарной дальности
которой — матрица частных производных от суммарной дальности  по элементам вектора состояния ИСЗ; блок
по элементам вектора состояния ИСЗ; блок 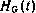 —матрица частных производных от
—матрица частных производных от  по координатам НИПов;
по координатам НИПов;  —белый шум с интенсивностью
—белый шум с интенсивностью  .
.
Изменение 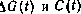 опишем простейшими формирующими фильтрами
опишем простейшими формирующими фильтрами 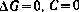 с начальными условиями
с начальными условиями
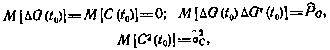
где 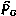 — априорная корреляционная матрица, задающая неопределенность координат НИПов;
— априорная корреляционная матрица, задающая неопределенность координат НИПов;  — дисперсия систематической ошибки измерений параметра
— дисперсия систематической ошибки измерений параметра  .
.
Фундаментальная матрица системы, описывающей эволюцию вектора 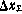 , имеет вид (для одного НИПа)
, имеет вид (для одного НИПа)

Рис. 4.1. Стандартная (а) и оптимальная (б) программы измерений
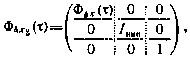
где  — единичная матрица размерности (3×3).
— единичная матрица размерности (3×3).
В качестве ограничения на точность определения орбиты примем ограничение на апостериорную дисперсию координаты  . На режим работы НИПов наложим ограничения, заключающиеся в том, что продолжительность одного сеанса измерений не должна превышать
. На режим работы НИПов наложим ограничения, заключающиеся в том, что продолжительность одного сеанса измерений не должна превышать  , а продолжительность интервала прогнозирования между двумя соседними сеансами для одного и того же НИПа —
, а продолжительность интервала прогнозирования между двумя соседними сеансами для одного и того же НИПа — 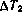 .
.
Расчеты проводились при следующих исходных данных. Параметры опорной орбиты:
r0=20 000 км,  = 20°, i =60°, u(t0)=0°. Ограничения
= 20°, i =60°, u(t0)=0°. Ограничения  принимались равными 10 и 180 мин соответственно. Длина мерного участка Т принималась равной трем суткам. На рис. 4.1 приведены примеры так называемой «стандартной» и оптимальной программ измерений, имеющие одну и ту же суммарную продолжительность измерений
принимались равными 10 и 180 мин соответственно. Длина мерного участка Т принималась равной трем суткам. На рис. 4.1 приведены примеры так называемой «стандартной» и оптимальной программ измерений, имеющие одну и ту же суммарную продолжительность измерений 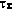 . Расчеты показывают, что в зависимости от значений
. Расчеты показывают, что в зависимости от значений  выигрыш в точности оценивания скалярного параметра
выигрыш в точности оценивания скалярного параметра  может составить от 10 до 40% (по апостериорному среднеквадратичному отклонению
может составить от 10 до 40% (по апостериорному среднеквадратичному отклонению  ).
).
ГЛАВА 5.
 2015-10-22
2015-10-22 652
652








