Численные методы программирования оптимального управления

В связи с тем, что задача программирования оптимального управления стохастической дискретной системой в общем случае может быть интерпретирована как специальная задача ма­тематического программирования, для ее численного решения мо­гут быть применены и соответствующие методы [28].

Ниже обсуждаются особенности применения для этой цели 'наи­более распространенных методов математического программирова­ния, таких, как градиентные методы и методы второго порядка.

Градиентные методы при отсутствии ограничений. Обратимся снова к задаче оптимизации программы управления системой

с целью минимизации терминального критерия

Как и прежде, считается, что начальное состояние х₀ известно. Предположим сначала, что ограничения на вектор управления отсутствуют.

Не стремясь здесь к получению точного решения с использова­нием условий оптимальности, рассмотрим процедуру приближен­ного решения задачи методом последовательных приближений, ос­нову которого составляет градиентный метод поиска.

Обозначим через , , 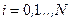q-e приближение иско­мой последовательности. Тогда в соответствии с градиентным ме­тодом [28] новое (q+1)-е приближение может быть найдено с по­мощью соотношения

где — градиент критерия оптимальности по вектору на q-й итерации; — шаг поиска.

Смысл данного соотношения заключается в том, что новое при­ближение управления получается путем перехода из старого приближения в направлении антиградиента 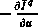с шагом .

Такое направление поиска, как известно, является локально наи­лучшим. В этом направлении минимизируемая функция имеет наи­большую скорость убывания.

Составляющие градиента могут быть определены чис­ленными методами как отношение приращения критерия к мало­му приращению (пробному) соответствующей составляющей управления .

Однако при таком подходе возникают настолько значительные вычислительные трудности, особенно при больших числах N и раз­мерностях т вектора управления ,что возможность получения решения становится сомнительной. Указанные трудности сущест­венно сокращаются, если обратиться к методу сопряженных си­стем. Напомним, что согласно этому методу вычисление градиента может быть осуществлено по формуле

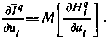
Здесь через обозначен гамильтониан на q-й итерации, равный

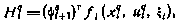
где в свою очередь вектор удовлетворяет сопряженной системе

Из приведенных соотношений видно, что для вычисления градиен­тов на каждой итерации необходимо вычислить математи­ческое ожидание производной гамильтониана по вектору управле­ния . А это может быть осуществлено путем совместного ста­тистического моделирования исходной системы (4.26) и сопряжен­ной (4.28).

Алгоритм такого моделирования состоит в следующем. С помо­щью датчика случайных чисел формируется конкретная j -я реали­зация последовательности случайных векторов , 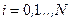. Далее при заданном начальном условии х₀ и известном управле­нии на q -итерации согласно (4.26) моделируется в прямом време­ни при изменении i от 0 до N j -я реализация фазовой траектории

Определив фазовый вектор в конечный момент и вычислив граничное значение сопряженного вектора

можем промоделировать и сопряженную систему в соответствии с(4.28):

Зная сопряженный вектор в j -й реализации, согласно можно вычислить градиент критерия в данной реализации:

Если теперь произвести осреднение по всем реализациям, то по­лучим градиент исходного критерия оптимальности по управлению на q -й итерации:

Здесь через k обозначено количество реализаций.

Основное преимущество метода сопряженных систем состоит в том, что в процессе моделирования для вычисления значения кри­терия оптимальности и набора градиентов для всех мо­ментов 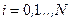в каждой реализации достаточно лишь один раз обратиться к системе (4.26) в прямом времени и к системе (4.28) - в обратном времени.

С целью улучшения процесса сходимости рассматриваемого градиентного метода при моделировании целесообразным оказы­вается применение зависимых испытаний, точнее, использование одних и тех же реализаций случайных векторов , , 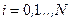на всех итерациях градиентного поиска. Такой способ моделирования является более экономичным, так как в конечном счете позволяет ограничиться существенно меньшим числом реализаций, чем при использовании независимых испытаний [26].

Шаг поиска может быть выбран различными способами. На­пример, при реализации простейшего градиентного метода он при­нимается постоянным, =const. При реализации метода наиско­рейшего спуска шаг выбирается наилучшим на данной итера­ции, т. е. из условия достижения критерием своего наименьшего значения в направлении антиградиента:

Учет ограничений на компоненты вектора управления. Часто в

задачах управления ограничения, накладываемые на компоненты вектора управления , имеют вид

где через 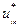обозначено предельное значение компоненты .

В этих случаях для поиска может быть использована следую­щая модификация градиентного метода, являющаяся по сути де­ла реализацией проективного градиентного метода [28].

Если точка является внутренней точкой допустимого множе­ства U или граничной, но с градиентом, направленным внутрь допустимого множества U, то переход к новому приближению осуществляется в соответствии с обычной схемой

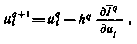
где градиент вычисляется по-прежнему согласно (4.27). Однако выбор шага поиска теперь следует проводить с учетом до­полнительного ограничения

где через обозначен максимально возможный на q-й итерации шаг поиска. Для его определения найдем сначала предельное зна­чение шага поиска 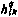, если принять во внимание только ограни­чения на компоненту управления :

Тогда с учетом всех ограничений будет равен

где через обозначено множество индексов i, k, для которых . Заметим, что равенство означает, что компонента принимает свое предельное значение, а градиент направлен во вне множества U.

Если множество окажется пустым, то это будет означать, что точка является граничной, а градиент направлен во вне до­пустимой области U. В этом случае переход к новому приближе­нию естественно осуществить по следующей схеме:

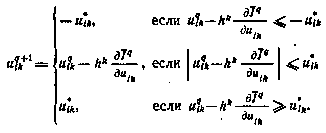
Смысл данной схемы состоит в том, что если при движении вдоль антиградиента какая-либо компонента вектора управления не выходит за пределы допустимого множества, то новое приближение по этой компоненте определяется согласно градиентному методу, если же при таком движении происходит выход за допус­тимое множество, то значение компоненты принимается равным прежнему предельному значению.

Оптимизация программы проведения однопараметрической коррекции. Проиллюстрируем возможность, применения изложен­ного метода на задаче оптимизации программы проведения однопараметрической коррекции космического аппарата. В качестве математической модели процесса коррекции, как и прежде, примем скалярное конечноразностное уравнение

Будем считать, что имеют место соотношения (4.16).

Требуется определить последовательность корректирующих воздействий , обращающих в минимум терминаль­ный критерий

В отличие от рассмотренного ранее случая полагаем, что «а каждое корректирующее воздействие накладывается ограничение .

Для получения точного решения задачи следовало бы восполь­зоваться необходимыми условиями оптимальности в форме диск­ретного принципа минимума. При этом задача оптимизации све­лась бы к некоторой краевой задаче, трудности решения которой обсуждались в предыдущем разделе. Если же получение точного решения не требуется, то для получения приближенного решения можно использовать изложенный выше градиентный метод. Вычис­лительный алгоритм такого метода в данном случае может быть представлен следующим образом.

1. Задается любое допустимое управление — начальное при­ближение .

2. Переход от произвольного q- го приближения к новому (q+1)- му осуществляется по схеме

где — шаг поиска, а вектор определяет направление поиска на q-й итерации.

3. Определение вектора на q-й итерации предполагает вы­полнение следующих операций:

1) определяется производная 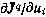на q-й итерации.

Так как в данном случае гамильтониан равен

то согласно (4.27) и (4.28) имеем

причем

Отсюда следует, что математическое ожидание сопряженной пере­менной для всех моментов времени есть величина постоянная и равная

Математическое ожидание конечного промаха в свою очередь может быть найдено на основании исходной модели движения

Заметим, что в силу линейности модели в данном случае при определении производных статистического моделирования проводить не требуется;

2) вычисляется максимально допустимый шаг поиска на q-й итерации согласно соотношениям

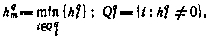
где

3) формируются компоненты вектора , определяющего на­правление поиска на q-й итерации:

4) выбор шага поиска hi можно осуществить наилучшим обра­зом, т. е. из условия

Причем характерно, что для вычисления значения самого кри­терия на q-й итерации можно воспользоваться уравнением для' второго момента текущего промаха , которое имеет вид

с граничным условием . При i = N+1 получаем .

Таким образом, в данной задаче удается избежать статистиче­ского моделирования на всех этапах поиска.

Применение методов второго порядка. Наиболее существенным недостатком всех градиентных методов (особенно при решении за­дач большой размерности) является медленная сходимость про­цесса поиска. В стохастических задачах, где в общем случае для вычисления как самой минимизируемой функции, так и ее произ­водных на каждой итерации должно производиться статистическое моделирование, этот недостаток еще более усугубляется. Одним из способов улучшения сходимости процесса поиска является учет при формировании нового приближения вторых производных кри­терия оптимальности, другими словами, использование методов второго порядка. Простейшим среди этих методов является метод Ньютона.

Его суть состоит в том, что в качестве нового (q+1)-го приближе­ния принимается оптимальное решение, обеспечивающее минимум квадратичной аппроксимации критерия оптимальности 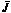на q-м приближении. Итак, квадратичная аппроксимация, получаемая путем разложения критерия 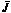в ряд Тейлора в окрестности q -го приближения, имеет вид

Произведя обычную минимизацию по вектору и путем приравни­вания нулю градиента , получаем

Предполагается, естественно, что ограничения на управления отсутствуют, а матрица положительно определенная, что обеспечивает, с одной стороны, существование обратной матрицы, а с другой стороны, гарантирует достижение в точке миниму­ма .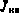

Покажем, что вычисление матриц вторых частных производных в каждой реализации может быть осуществлено, как и вычисление составляющих градиента при использовании сопряженных систем, путем однократного обращения к некоторой системе уравнений.

С этой целью продифференцируем дважды терминальный кри­терий по текущему управлению . Дифференцируя в свое время этот критерий один раз, получали следующие соотно­шения, справедливые для каждой реализации:

где

Для определения элементов матрицы вторых частных производ­ных продифференцируем 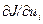еще один раз по .

Учитывая при этом (4.30), получим следующее соотношение:

которое можно представить в более компактном виде

если ввести в рассмотрение обозначения

Аналогично для матрицы смешанных производных в предполо­жении j>i будем иметь

или в компактной форме

где — матрицы, удовлетворяющие рекуррентному соотношению

Таким образом, на основании соотношений (4.31) — (4.34) с граничными условиями на правом конце путем однократного про­счета в обратном времени можно получить значения всех элемен­тов матрицы вторых частных производных 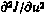в конкретной реа­лизации. Используя далее метод статистического моделирования по описанной ранее схеме и произведя осреднение по совокупности реализаций, получаем матрицу в алгоритме (4.29).

Хорошо известно [28], что метод Ньютона, имея большую скорость сходимости, чем градиентные методы, обладает лишь локальной сходимостью. Это значит, что метод обеспечивает сходимость процесса поиска к оптимальному решению при условии выбора достаточно хорошего начального приближения. В противном слу­чае метод может оказаться расходящимся. Для придания методу свойства глобальной сходимости по аналогии с градиентными ме­тодами вводят шаг поиска на каждой итерации , и схема, теперь уже модифицированного метода Ньютона, принимает вид

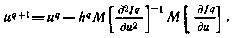
Шаг поиска может выбираться разными способами, например, из условия

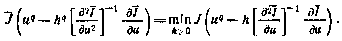
Естественно, что при больших числах N, а значит, и при боль­ших размерностях вектора и вычисление полной матрицы может потребовать значительных затрат машинного времени. Для их сокращения можно рекомендовать использование приема погрупповой оптимизации, согласно которому последующее приближение получается из предыдущего варьированием компонент вектора уп­равления лишь в один единственный i -й момент времени при фик­сированных значениях управлений в другие моменты. Затем после­довательно варьируются и другие векторы. При такой погрупповой оптимизации алгоритм (4.29) принимает вид

Простота данного алгоритма состоит в том, что он не требует вычисления матриц вторых смешанных производных 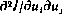, , с которыми и связаны основные вычислительные трудности. Вычисление матриц не вызывает затруднений.

Иногда может оказаться полезным и другой, еще более простой алгоритм поиска, предполагающий, что матрица яв­ляется диагональной. В этом случае для каждой j -й компоненты вектора получаем следующую расчетную формулу:

С одной стороны, как только что было установлено, этот алго­ритм может рассматриваться как частный случай модифицирован­ного метода Ньютона. С другой стороны, он может интерпретиро­ваться как одна из разновидностей градиентных методов, в кото­рой поиск осуществляется в пространстве управлений с перемен­ной на каждой итерации метрикой.

Параметрическая оптимизация закона коррекции. Проиллюст­рируем применение методов второго порядка снова на задаче, свя­занной с оптимизацией процесса коррекции космического аппара­та путем определения коэффициентов обратной связи 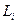в зависи­мости .

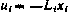Как и прежде, математическую модель процесса коррекции и критерий оптимальности представим в виде

Сначала преобразуем данную задачу к задаче терминального управления. С этой целью введем вспомогательную переменную 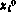, определив ее с помощью уравнения

Тогда критерий оптимальности становится терминальным в прост­ранстве

Теперь для решения задачи обратимся к алгоритму (4.35). В дан­ном случае гамильтониан имеет вид

а сопряженные переменные удовлетворяют уравнениям

и

откуда следует, что

Как и прежде, производная критерия оптимальности 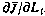, равная согласно (4.30)

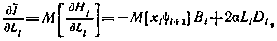
может быть приведена к виду

где определяются согласно (4.23) - (4.25), а второй момент согласно соотношению

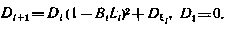
Найдем теперь выражение для второй производной . Рас­крывая (4.31), с учетом (4.32) в данном случае можно получить

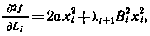
где определяется с помощью рекуррентного соотношения

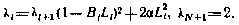
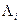Нетрудно заметить, что матрицы и связаны условием

Учитывая это, получаем

Анализируя полученные выражения, можно установить, что не зависит от текущего параметра 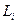, хотя зависит от всех последующих при j>i.

Поэтому целесообразно оптимизацию по отдельным компонен­там искомой последовательности проводить в такой очередности: j =N, N—1,..., 1. Оказывается, что применение алгоритма (4.35) в этом случае позволяет за один цикл итераций по всем 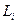, i = N,..., 1, найти сразу точное решение задачи. Действительно, получаем

Учитывая данный результат, можно рекомендовать и при реше­нии более сложных задач, в частности, при оптимизации нелиней­ных систем погрупповой поиск управляющих воздействий осуще­ствлять в очередности j = N, N -1,..., 1.