Решение задач, связанных с оптимизацией непрерывных как стохастических, так и детерминированных систем, практически всегда требует дискретизации. Можно указать два подхода к такой дискретизации.
Первый состоит в переходе от исходной непрерывной задачи к дискретной сразу до ее решения. При этом дифференциальные уравнения, описывающие поведение системы, заменяются конечно-разностными. Соответствующим образом преобразуется и критерий оптимальности. Для решения полученной вновь задачи могут быть применены либо условия оптимальности для дискретных систем, либо соответствующие численные методы поиска оптимального управления.
Второй подход связан с использованием необходимых условий оптимальности, полученных непосредственно для исходной непрерывной задачи. Эти условия в явном виде редко позволяют получить решение задачи оптимизации. Они обычно лишь трансформируют исходную задачу в некоторую другую, например связанную с решением краевой задачи для системы дифференциальных уравнений, при решении которой в конечном счете приходится проводить также дискретизацию.
Заранее бывает трудно отдать предпочтение какому-либо одному из этих подходов. Первый подход, очевидно, более прост в реализации при получении численного решения задачи, обладает определенной универсальностью, так как фактически исходную задачу сводит,к специальной задаче.математического программирования, для решения которой в настоящее время накоплен богатый опыт. Однако применение второго подхода иногда позволяет более просто выявить структуру оптимального управления, а в некоторых случаях и найти более эффективный способ решения задачи в целом.
Учитывая это, рассмотрим необходимые условия оптимальности в задаче программирования оптимального управления непрерывной стохастической системой и их применение для решения конкретных задач.
Пусть динамическая система на интервале времени [0, Т] описывается следующим стохастическим дифференциальным уравнением

где x=x(t), u = u(t) —векторы состояния и управления соответственно в текущий момент,  , U — множество допустимых управлений;
, U — множество допустимых управлений; 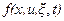 —вектор-функция, непрерывно дифференцируемая по своим аргументам;
—вектор-функция, непрерывно дифференцируемая по своим аргументам;  —случайный процесс; с известными статистическими характеристиками.
—случайный процесс; с известными статистическими характеристиками.
Задача программирования оптимального управления заключается в отыскании такой временной зависимости u(t), которая обеспечивает перевод системы (4.36) из заданного начального состояния х(0)=х0 в некоторое конечное состояние х(Т) с минимальным значением критерия

Наиболее просто необходимые условия оптимальности для сформулированной задачи получаются в предположении, что непрерывные случайные процессы  и x(t) могут быть представлены в виде дискретных последовательностей случайных векторов
и x(t) могут быть представлены в виде дискретных последовательностей случайных векторов 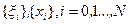 , которые при стремлении интервала дискретности Δ к нулю стягиваются к исходным процессам
, которые при стремлении интервала дискретности Δ к нулю стягиваются к исходным процессам  и x(t). В этом случае для малых Δ (с точностью до членов первого порядка малости) вместо уравнения (4.36) и критерия (4.37) можно записать их конечно-мерные аналоги
и x(t). В этом случае для малых Δ (с точностью до членов первого порядка малости) вместо уравнения (4.36) и критерия (4.37) можно записать их конечно-мерные аналоги
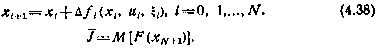
Исходная задача, таким образом, в первом приближении оказывается эквивалентной задаче программирования оптимального управления  , изученной нами ранее. Поэтому для нее необходимые условия оптимальности можно выписать. С этой целью составим гамильтониан для этой задачи, обозначая его через
, изученной нами ранее. Поэтому для нее необходимые условия оптимальности можно выписать. С этой целью составим гамильтониан для этой задачи, обозначая его через 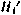 :
:

где сопряженный вектор 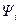 удовлетворяет при этом уравнению
удовлетворяет при этом уравнению
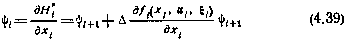
при граничном условии
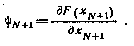
Тогда, если  — оптимальная последовательность, то согласно (4.10) имеют место следующие условия:
— оптимальная последовательность, то согласно (4.10) имеют место следующие условия:
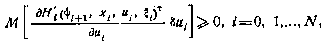
для всех допустимых  т. е. удовлетворяющих условию
т. е. удовлетворяющих условию 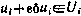 .
.
Смысл этих условий состоит в неотрицательности вариации 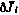 терминального критерия
терминального критерия 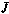 , получаемой за счет вариации управления
, получаемой за счет вариации управления 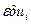 в i -й момент:
в i -й момент:

Установим связь вариации 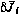 с вариацией
с вариацией  фазового вектора
фазового вектора 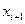 , вызываемой в свою очередь вариацией управления
, вызываемой в свою очередь вариацией управления 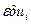 . С этой целью примем, что вариации управления во все другие моменты времени, кроме i -го, равны нулю, т. е.
. С этой целью примем, что вариации управления во все другие моменты времени, кроме i -го, равны нулю, т. е.  при
при 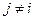 , а
, а 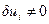 . Тогда для моментов
. Тогда для моментов  вариация
вариация 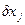 вектора
вектора  будет тождественно равна нулю. Для момента j = i+1 в соответствии с уравнением (4.38) будем иметь
будет тождественно равна нулю. Для момента j = i+1 в соответствии с уравнением (4.38) будем иметь
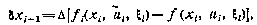
а для моментов j>i +l вектор 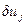 удовлетворяет уравнению в отклонениях
удовлетворяет уравнению в отклонениях

Здесь через  обозначено любое допустимое управление
обозначено любое допустимое управление 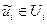 в отличие от оптимального управления
в отличие от оптимального управления  .
.
Покажем, что скалярное произведение вектора 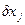 , определяемого уравнением (4.41), и сопряженного вектора
, определяемого уравнением (4.41), и сопряженного вектора 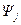 , определяемого в соответствии с (4.39), представляет собой постоянную величину для любых
, определяемого в соответствии с (4.39), представляет собой постоянную величину для любых 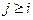 . Действительно, согласно (4.39) и (4.41)
. Действительно, согласно (4.39) и (4.41)

Но для момента j = N+1 согласно (4.38), (4.39) математическое ожидание этого произведения определяет вариацию критерия оптимальности
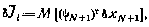
которая должна быть неотрицательной. Поэтому условие оптимальности (4.40) можно представить так:
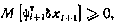
или, раскрывая вариацию 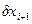 вектора
вектора 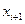 , в развернутом виде
, в развернутом виде

Полученное соотношение, как уже было установлено, справедливо для любого допустимого управления 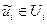 и для любого момента времени
и для любого момента времени 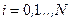 . Если теперь ввести в рассмотрение новый гамильтониан в виде
. Если теперь ввести в рассмотрение новый гамильтониан в виде
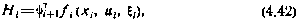
то условию оптимальности можно придать следующий вид:

или окончательно

Таким образом, для дискретной системы (4.38) при малых значениях интервала дискретности оказывается справедливым дискретный принцип минимума по отношению к гамильтониану (4.42) независимо от свойства гамильтониана и допустимого множества  .
.
Осуществим теперь предельный переход во всех соотношениях, определяющих необходимые условия оптимальности. Для этого устремим интервал дискретности Δ к нулю. Соотношения (4.38) примут вид исходного дифференциального уравнения (4.36) и исходного критерия (4.37), а конечно-разностное уравнение (4.39) для сопряженного вектора 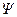 перейдет в дифференциальное уравнение
перейдет в дифференциальное уравнение

с граничным условием

Необходимые условия оптимальности (4.43) примут вид непрерывного принципа минимума

где гамильтониан

Смысл условия (4.45) заключается в том, что при оптимальном управлении в каждый момент времени математическое ожидание гамильтониана достигает своего минимального (по управлению) значения. С учетом вида гамильтониана (4.46) уравнение для сопряженного вектора можно записать в виде

Благодаря принципу минимума (4.45), исходная задача определения оптимальной программы управления u(t) из условия минимизации функционала (4.37) редуцируется к краевой задаче для системы стохастических уравнений (4.36) и (4.47). Для исходных уравнений (4.36) граничное условие x(0) задано «слева», т. е. в начальный момент, а для сопряженных уравнений (4.47) — «справа», т. е. в конечный момент времени в виде условия (4.44). Оптимальное управление должно удовлетворять этим краевым условиям и одновременно обращать в минимум математическое ожидание гамильтониана.
Если, как и при рассмотрении дискретного случая, в качестве граничного условия для сопряженного вектора принять условие 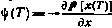 , т. е. изменить в условии (4.44) знак на обратный, то необходимое условие оптимальности (4.45) примет более привычную форму принципа максимума:
, т. е. изменить в условии (4.44) знак на обратный, то необходимое условие оптимальности (4.45) примет более привычную форму принципа максимума:

Если в исходной задаче критерий оптимальности имеет более сложную интегротерминальную структуру вида
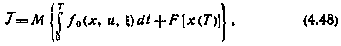
то путем введения дополнительной переменной  , определяемой с помощью дифференциального уравнения
, определяемой с помощью дифференциального уравнения

критерий (4.48) сразу сводится к терминальному виду
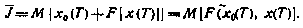
по отношению к вектору состояния х и дополнительной переменной  совместно.
совместно.
Составим гамильтониан для данной расширенной задачи:

Здесь сопряженная компонента  удовлетворяет уравнению
удовлетворяет уравнению
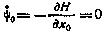
при граничном условии  . Следовательно,
. Следовательно,  является неслучайной постоянной величиной
является неслучайной постоянной величиной 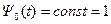 . Поэтому гамильтониан в данном случае представляется в форме
. Поэтому гамильтониан в данном случае представляется в форме
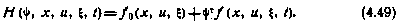
Уравнение для сопряженного вектора 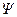 согласно (4.44) принимает вид
согласно (4.44) принимает вид

Граничные условия для сопряженного вектора 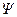 сохраняют прежний вид, т. е. имеет место равенство (4.44).
сохраняют прежний вид, т. е. имеет место равенство (4.44).
Таким образом, для задачи оптимального управления системой (4.36) с критерием вида (4.48) необходимые условия оптимальности имеют тот же самый вид (4.45) с учетом (4.47), (4.44), что и для задачи с терминальным критерием (4.37), за исключением лишь вида самого гамильтониана. Теперь он имеет вид (4.49) вместо (4.46).
Обсудим частный случай задачи управления — детерминированный, т. е. случай, когда отсутствуют какие-либо возмущения: х(0) — известно;  . Характерная особенность этого случая состоит в том, что как векторы x(t) и
. Характерная особенность этого случая состоит в том, что как векторы x(t) и  , так и сам гамильтониан теперь являются неслучайными. Необходимые условия оптимальности упрощаются. В них опускается операция математического ожидания, поскольку математическое ожидание неслучайной величины есть сама величина. Например, для случая управления терминальным состоянием они принимают вид
, так и сам гамильтониан теперь являются неслучайными. Необходимые условия оптимальности упрощаются. В них опускается операция математического ожидания, поскольку математическое ожидание неслучайной величины есть сама величина. Например, для случая управления терминальным состоянием они принимают вид
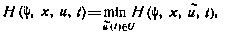
где вектор 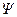 определяется путем решения краевой задачи для исходной системы уравнений
определяется путем решения краевой задачи для исходной системы уравнений
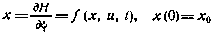
и сопряженной
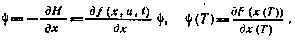
 2015-10-22
2015-10-22 719
719








