Проиллюстрируем применение необходимых условий оптимальности на примере решения задачи оптимизации процесса коррекции космического аппарата с целью минимизации конечной ошибки по какому-либо одному параметру траектории.
Обозначим через х величину конечной ошибки, называемую для краткости промахом; через  — промах, прогнозируемый в момент, предшествующий проведению i -й коррекции; через
— промах, прогнозируемый в момент, предшествующий проведению i -й коррекции; через  — величину i -ro корректирующего воздействия; через
— величину i -ro корректирующего воздействия; через 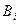 — функцию влияния i -ro корректирующего воздействия на прогнозируемый промах,
— функцию влияния i -ro корректирующего воздействия на прогнозируемый промах, 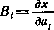 . Совершенно очевидно, что функция
. Совершенно очевидно, что функция 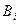 связанна с моментом проведения i -й коррекции и зависит от него. Тогда в качестве математической модели процесса коррекции в первом приближении можно принять скалярное дискретное уравнение
связанна с моментом проведения i -й коррекции и зависит от него. Тогда в качестве математической модели процесса коррекции в первом приближении можно принять скалярное дискретное уравнение
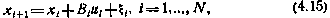
где 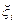 — случайное возмущение, обусловленное ошибками траекторных измерений и ошибками реализации корректирующего воздействия
— случайное возмущение, обусловленное ошибками траекторных измерений и ошибками реализации корректирующего воздействия  ; N — число коррекций.
; N — число коррекций.
Полагаем, что статистические характеристики случайного возмущения заданы и имеют вид
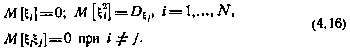
Считается, что прогнозируемый априори (до совершения каких-либо коррекций) промах, равный по определению величине  , известен.
, известен.
Рассмотрим сначала задачу оптимизации программы проведения коррекций, в которой требуется найти последовательность корректирующих воздействий  , обеспечивающую при заданных энергетических возможностях минимум конечного промаха. В качестве критерия оптимальности примем величину второго момента конечного промаха
, обеспечивающую при заданных энергетических возможностях минимум конечного промаха. В качестве критерия оптимальности примем величину второго момента конечного промаха 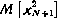 .
.
Энергетические возможности будем оценивать суммой квадратов всех корректирующих импульсов, считая, что должно иметь место условие
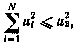
где 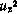 — заданная величина.
— заданная величина.
Заметим, что в рассматриваемой задаче ограничения, накладываемые непосредственно на управления  , отсутствуют. Учет ограничения на энергетические затраты осуществим с помощью обобщенного метода множителей Лагранжа [28]. Сущность этого метода базируется на известном свойстве, заключающемся в том, что необходимые условия оптимальности исходной задачи при наличии ограничений совпадают с необходимыми условия-ми оптимальности новой задачи, но уже без ограничений. Последняя отличается от исходной задачи лишь критерием оптимальности. В качестве нового (обобщенного) критерия оптимальности выступает функция Лагранжа. Применительно к рассматриваемому примеру таким обобщенным критерием оптимальности является интегротерминальный критерий
, отсутствуют. Учет ограничения на энергетические затраты осуществим с помощью обобщенного метода множителей Лагранжа [28]. Сущность этого метода базируется на известном свойстве, заключающемся в том, что необходимые условия оптимальности исходной задачи при наличии ограничений совпадают с необходимыми условия-ми оптимальности новой задачи, но уже без ограничений. Последняя отличается от исходной задачи лишь критерием оптимальности. В качестве нового (обобщенного) критерия оптимальности выступает функция Лагранжа. Применительно к рассматриваемому примеру таким обобщенным критерием оптимальности является интегротерминальный критерий
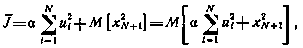
где  — множитель Лагранжа,
— множитель Лагранжа,  . Определение множителя а осуществляется после решения задачи минимизации критерия
. Определение множителя а осуществляется после решения задачи минимизации критерия 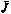 по
по  при фиксированном
при фиксированном  из условия
из условия
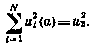
Здесь через  обозначено оптимальное решение при фиксированном значении
обозначено оптимальное решение при фиксированном значении  . Для отыскания этого решения обратимся к необходимым условиям оптимальности. Составим согласно (4.14) гамильтониан, соответствующий обобщенному критерию оптимальности:
. Для отыскания этого решения обратимся к необходимым условиям оптимальности. Составим согласно (4.14) гамильтониан, соответствующий обобщенному критерию оптимальности:
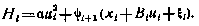
Так как условия выпуклости 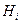 по
по  в данном случае выполнены, то имеет место дискретный принцип минимума (4.12). Если бы на управляющие (корректирующие) воздействия
в данном случае выполнены, то имеет место дискретный принцип минимума (4.12). Если бы на управляющие (корректирующие) воздействия  накладывались дополнительные ограничения, то операцию минимума в (4.12)
накладывались дополнительные ограничения, то операцию минимума в (4.12)
следовало бы раскрывать с учетом этих ограничений. В данном же случае таких ограничений нет. Поэтому для достижения минимума в (4.12) необходимо и достаточно выполнения условия
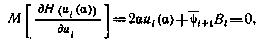
где через  обозначено математическое ожидание сопряженной переменной
обозначено математическое ожидание сопряженной переменной  . Из этого условия получаем связь оптимального управления,с неизвестным пока множителем Лагранжа а и сопряженной переменной
. Из этого условия получаем связь оптимального управления,с неизвестным пока множителем Лагранжа а и сопряженной переменной  :
:

Согласно (4.14) находим
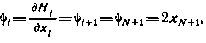
откуда следует, что 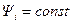 и поэтому
и поэтому  , а оптимальное управление выражается через математическое ожидание конечного промаха
, а оптимальное управление выражается через математическое ожидание конечного промаха

Из последнего выражения следует, что при а = 0 задача оказывается вырожденной. Это связано с тем, что  = 0 соответствует случаю неограниченных энергетических возможностей. Естественно, что при этом и управление оказывается неограниченным. В этом случае нет необходимости в проведении нескольких коррекций, ибо сразу можно устранить любой ожидаемый промах. Поэтому в дальнейшем будем считать, что
= 0 соответствует случаю неограниченных энергетических возможностей. Естественно, что при этом и управление оказывается неограниченным. В этом случае нет необходимости в проведении нескольких коррекций, ибо сразу можно устранить любой ожидаемый промах. Поэтому в дальнейшем будем считать, что  >0.
>0.
Учитывая полученную структуру управления, на основании исходного уравнения (4.15) с учетом (4.16) нетрудно установить связь ожидаемого промаха 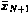 c неизвестным пока множителем
c неизвестным пока множителем  :
:
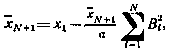
откуда
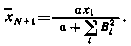
С учетом последнего соотношения оптимальное управление принимает вид
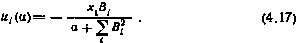
Это выражение с точностью до константы (множителя  ) и дает решение поставленной задачи по определению оптимальной программы проведения коррекций.
) и дает решение поставленной задачи по определению оптимальной программы проведения коррекций.
Следует отметить, что при заданных статистических свойствах возмущения (4.16) решение задачи оказалось инвариантным по отношению к этому возмущению. Другими словами оно полностью совпадает с решением соответствующей детерминированной задачи, когда считается 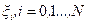 .
.
Как уже указывалось, множитель  должен быть определен из условия
должен быть определен из условия  , которое с учетом найденного управления(4.17) легко сводится к квадратному относительно
, которое с учетом найденного управления(4.17) легко сводится к квадратному относительно  уравнению
уравнению
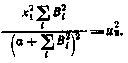
Неотрицательный корень этого уравнения равен

причем  >0 имеет место лишь при условии
>0 имеет место лишь при условии 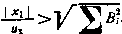 .
.
Учитывая комментарий, сделанный ранее относительно случая  =0, последнее условие можно интерпретировать, как условие целесообразности проведения нескольких коррекций (во всяком случае, более одной).
=0, последнее условие можно интерпретировать, как условие целесообразности проведения нескольких коррекций (во всяком случае, более одной).
Подставляя найденное значение в (4.17), окончательно получаем оптимальное управление
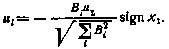
При решении данной задачи, предполагалось, что моменты проведения коррекций или, что то же самое, коэффициенты 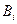 заданы. Получив решение при фиксированных
заданы. Получив решение при фиксированных 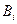 и установив зависимость критерия оптимальности от этих коэффициентов, можно поставить задачу и об определении оптимальных моментов проведения коррекции. Эта задача является классической задачей математического программирования и может быть решена соответствующими методами [28].
и установив зависимость критерия оптимальности от этих коэффициентов, можно поставить задачу и об определении оптимальных моментов проведения коррекции. Эта задача является классической задачей математического программирования и может быть решена соответствующими методами [28].
При решении задачи оптимизации программы проведения корректирующих воздействий полагалось, что в процессе реализации этих воздействий никакая информация использована быть не может. Более типичным случаем является использование при проведении коррекции информации о траекторию измерениях. Оказывается, что в этом случае задачу оптимизации также можно сформулировать как задачу программирования оптимального управления (правда, это будет совсем другая задача), если заранее задаться структурой управления. В качестве примера рассмотрим типичный случай, когда корректирующее воздействие формируется пропорционально величине прогнозируемого промаха:

Знак минус в выражении (4.18) введен для того, чтобы подчеркнуть использование принципа обратной связи в процессе коррекции.
Задачу оптимизации сформулируем следующим образом: найти последовательность коэффициентов 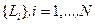 , которые с учетом закона коррекции (4.18) и в силу уравнения (4.15) обеспечат минимум терминальному критерию
, которые с учетом закона коррекции (4.18) и в силу уравнения (4.15) обеспечат минимум терминальному критерию 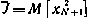 при условии
при условии 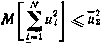 .
.
Отметим, что последнее условие, как и ранее, учитывает ограничение на энергетику, но в отличие от рассмотренного случая содержит теперь операцию математического ожидания. Дело в том, что в задаче программирования, рассмотренной ранее, любое управление  было неслучайно и поэтому ограничение на энергетику
было неслучайно и поэтому ограничение на энергетику  носило неслучайный характер. Теперь же управляющее воздействие согласно (4.18) носит случайный характер в силу случайности каждого
носило неслучайный характер. Теперь же управляющее воздействие согласно (4.18) носит случайный характер в силу случайности каждого  . Поэтому и ограничения на энергетику также принимают случайный характер. Его учет может быть различным. Можно потребовать выполнения этого условия, например, по вероятности. А можно поступить более просто, заменив левую часть в ограничении соответствующим математическим ожиданием. Именно таким приемом мы и воспользовались. При этом, конечно, следует иметь в виду, что ограничение
. Поэтому и ограничения на энергетику также принимают случайный характер. Его учет может быть различным. Можно потребовать выполнения этого условия, например, по вероятности. А можно поступить более просто, заменив левую часть в ограничении соответствующим математическим ожиданием. Именно таким приемом мы и воспользовались. При этом, конечно, следует иметь в виду, что ограничение  будет удовлетворяться лишь в среднем.
будет удовлетворяться лишь в среднем.
Для решения задачи перепишем модель процесса коррекции (4.15) с учетом (4.18):
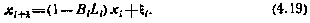
Как и прежде, перейдем к обобщенному критерию оптимальности, который теперь принимает вид
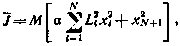
где  — также множитель Лагранжа, подлежащий в дальнейшем определению,
— также множитель Лагранжа, подлежащий в дальнейшем определению,  .
.
Воспользуемся необходимыми условиями оптимальности. Составим для этого согласно (4.14) гамильтониан.
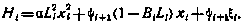
При оптимальных значениях 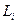 сопряженная переменная
сопряженная переменная 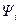 в соответствии с (4.14) удовлетворяет следующему уравнению:
в соответствии с (4.14) удовлетворяет следующему уравнению:
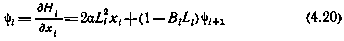
с граничным условием
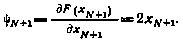
Так как ограничения на коэффициенты 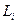 отсутствуют, то согласно (4.11) необходимые условия оптимальности принимают вид
отсутствуют, то согласно (4.11) необходимые условия оптимальности принимают вид

Здесь через  обозначен второй момент промаха
обозначен второй момент промаха  . В соответствии с уравнением (4.19)
. В соответствии с уравнением (4.19)  может быть определен с помощью уравнения
может быть определен с помощью уравнения

Так как считается, что априорный промах  известен, то имеем следующее граничное (начальное) условие:
известен, то имеем следующее граничное (начальное) условие:
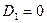
Отсюда видно, что  зависит от значений коэффициентов
зависит от значений коэффициентов  лишь в предшествующие моменты j= 1,..., i —1 и не зависит от
лишь в предшествующие моменты j= 1,..., i —1 и не зависит от 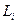 .
.
Основная трудность использования условия оптимальности (4.21) состоит в необходимости раскрытия математического ожидания 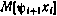 , зависящего от искомого значения
, зависящего от искомого значения 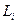 . Установим эту зависимость. Используя временно для краткости обозначение
. Установим эту зависимость. Используя временно для краткости обозначение
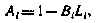
перепишем уравнения (4.19) и (4.20) в виде

На основании этих уравнений можно записать следующее выражение для сопряженной переменной  :
:
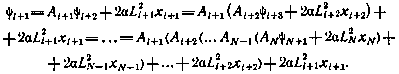
Образуем произведение 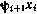 , учитывая, что
, учитывая, что  и произведем статистическое осреднение его:
и произведем статистическое осреднение его:
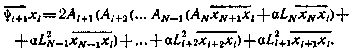
Теперь учтем, что для любого 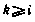 имеет место соотношение
имеет место соотношение

Получим

Если теперь ввести в рассмотрение параметр 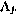 , определив его с помощью рекуррентного соотношения
, определив его с помощью рекуррентного соотношения
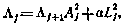
или в развернутом виде

с граничным условием 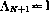 , то выражению (4.22) можно придать следующую компактную форму:
, то выражению (4.22) можно придать следующую компактную форму:
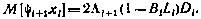
Подставляя его в условие оптимальности (4.21), получаем окончательно уравнение для определения оптимальных значений 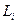 .
.
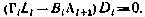
Здесь введено обозначение

Так как в общем случае  , то оптимальное значение параметра
, то оптимальное значение параметра 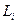 должно быть равно
должно быть равно

С учетом выражений (4.23), (4.24) рекуррентное соотношение для параметра 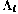 , преобразуется к виду
, преобразуется к виду

Таким образом, задача определения оптимальных значений 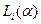 сведена к последовательному применению рекуррентного соотношения (4.25) с учетом (4.23), (4.24). Решение заканчивается определением множителя
сведена к последовательному применению рекуррентного соотношения (4.25) с учетом (4.23), (4.24). Решение заканчивается определением множителя  из условия
из условия
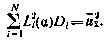
 2015-10-22
2015-10-22 406
406








