Для получения формулы прямоугольников интервал интегрирования [ a, b ] разбивается на n подынтервалов равной длины (шагов) точками: x 0 = a, x 1, x 2, …, xi, xi +1, …, xn = b так, что
xi +1 - xi = h = 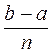 , i = 1, 2, …, n. (2)
, i = 1, 2, …, n. (2)
На этих подынтервалах строятся прямоугольники, высота их определяется значением функции f (x) в какой либо точке подынтервала.
Если f (xi) определяется для левой границы каждого подынтервала (рис. 2.1), то формула прямоугольников имеет следующий вид:
I1 = 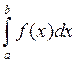 ≈
≈ 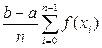 (3)
(3)
и называется формулой левых прямоугольников.
Если f (xi) определяется для правой границы каждого подынтервала (рис. 2), то
I2 = 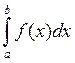 ≈
≈ 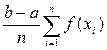 (4)
(4)
и называется формулой правых прямоугольников.
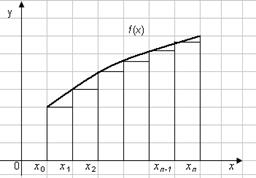

Рис. 1 Рис. 2
Если функция монотонна на отрезке [ a, b ], то в одном случае получается значение интеграла I с недостатком I1, а в другом – с избытком I2. Более точное значение I получают при усреднении величин:
I = 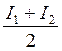 . (5)
. (5)
Если f (xi) определяется для середины каждого подынтервала, то формула прямоугольников имеет следующий вид:
I3 = 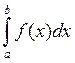 ≈
≈ 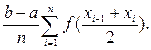 (6)
(6)
и называется формулой средних прямоугольников.
Точность интегрирования для этих методов приближенно равняется ε ≈ h.
Пример.
С помощью формул левых, правых и средних прямоугольников вычислить 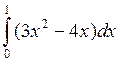 , если h = 0,2.
, если h = 0,2.
Точное решение: 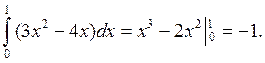
?Вычисление интеграла 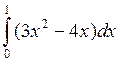 методом прямоугольников выполним в таблице Excel (рис. 3, 3- a).
методом прямоугольников выполним в таблице Excel (рис. 3, 3- a).
Значения интервала интегрирования [0, 1] соответственно поместить в ячейки B3 и F3. Интервал интегрирования разобьем на 5 подынтервалов (n = 5). Введем значение n в ячейку В2. Шаг интегрирования вычислим в ячейке F2 по формуле
h = 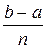 → h =
→ h = 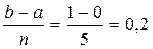 .
.
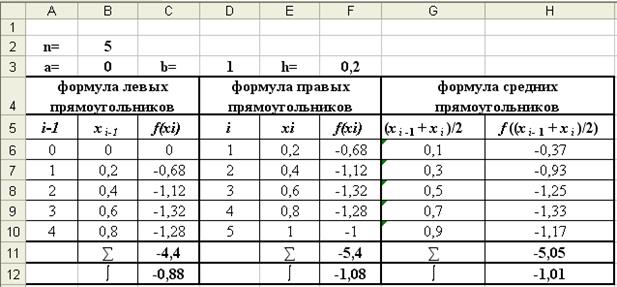
Рис. 3 (Режим решения)
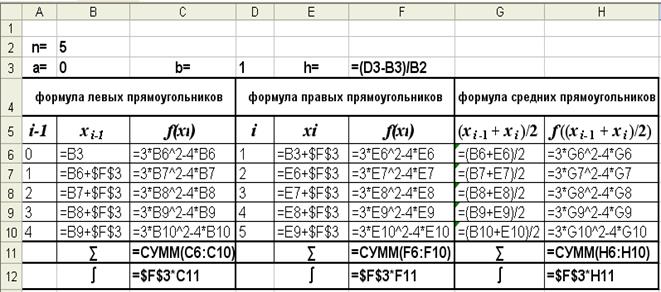
Режим показа формул
Рис. 3 - а
I) Для приближенного вычисления интеграла по формуле левых прямоугольников (3) требуется вычислить значения функции f (x) = 3 x 2 - 4 x в точках (2):
x 0 = a= 0;
x 1= x 0 + h= 0+0,2 =0,2;
x 2 = x 1 + h = 0,2 + 0,2 = 0,4;
x 3 = x 2+ h = 0,4 + 0,2 = 0,6;
x 4 = x3+h = 0,6 + 0,2 = 0,8.
Вычисление значений x 0, x 1, x 2, x 3, x 4, представлено в блоке ячеек B6:B10, а соответствующие им значения функции – в блоке ячеек С6:С10.
Затем следует вычислить их сумму (в ячейке С11) и полученное значение умножить на шаг интегрирования h (в ячейке С12):
|
I =.
II) Для приближенного вычисления интеграла по формуле правых прямоугольников (4) требуется вычислить значения функции f (x) = 3 x 2 - 4 x в точках:
x 1= x 0 + h= 0 + 0,2 = 0,2;
x 2 = x 1 + h = 0,2 + 0,2 = 0,4;
x 3 = x 2+ h = 0,4 + 0,2 = 0,6;
x 4 = x 3 +h = 0,6 + 0,2 = 0,8.
x 5 = x 4 +h = 0,8 + 0,2 = 1,0.
Вычисление значений x 1, x 2, x 3, x 4, x 5 представлено в блоке ячеек Е6:Е10, а соответствующие им значения функции – в блоке ячеек F6:F10.
Затем следует вычислить их сумму (в ячейке F11) и полученное значение умножить на шаг интегрирования h (в ячейке F12):
Приближенное значение интеграла, вычисленное по формуле левых прямоугольников равно -0,88, а по формуле правых прямоугольников равно -1,08.
Их среднее значение ближе к точному, равному -1.
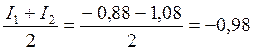
III) Для приближенного вычисления интеграла по формуле средних прямоугольников (5) требуется вычислить значения функции f (x) = 3 x 2 - 4 x в точках:
(xi -1+ x i)/2 (блок ячеек G6:H12), их сумму (ячейка H11), полученное значение умножить на шаг интегрирования h (ячейка H12).
Разбивая интервал интегрирования на большее число отрезков, например, на 10, можно получить более точное решение (рис. 4).?

Рис. 4
Для получения формулы трапеций интервал интегрирования [ a, b ] разбивается на n подынтервалов равной длины (шагов) точками: x 0 = a, x 1, x 2, …, xi, xi +1, …, xn = b так, что
xi +1 - xi = h = 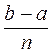 , i = 1, 2, …, n.
, i = 1, 2, …, n.
На каждом отрезке (xi, xi +1) дугу Xi Xi +1 графика подынтегральной функции y = f (x) заменяют стягивающей ее хордой (рис. 2.5) и вычисляют площади трапеций xiXi Xi +1 xi +1, высота которых равна h, а основания определяются значением функции f (xi), f (xi+1).
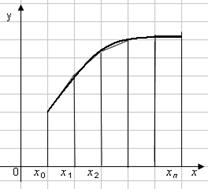
Рис. 2.5
Так как площадь трапеции равняется полусумме оснований, умноженной на высоту, интеграл приближенно равен сумме площадей всех полученных трапеций:
 =
=
=  =
=
= 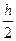 [ f (x 0) + 2 f (x 1) + 2 f (x 2)+…+ + 2 f (xn- 1) + f (xn)]=
[ f (x 0) + 2 f (x 1) + 2 f (x 2)+…+ + 2 f (xn- 1) + f (xn)]=
= 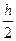 [ f (xa) + 2 f (x 1) + 2 f (x 2)+…+ + 2 f (xn- 1) + f (xb)]=
[ f (xa) + 2 f (x 1) + 2 f (x 2)+…+ + 2 f (xn- 1) + f (xb)]=
= 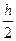 [ f (xa) + f (xb) +
[ f (xa) + f (xb) +  ]. (7)
]. (7)
Таким образом, формула трапеций имеет вид:
I = 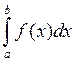 ≈
≈ 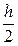
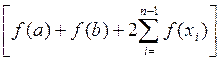 . (8)
. (8)
Точность интегрирования для этого метода приближенно равняется ε ≈ h2.
Пример (продолжение).?Пользуясь формулой трапеций, вычислить  при h = 0,2.
при h = 0,2.
Решение. Вычисление интеграла 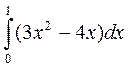 методом трапеций (8) выполним в таблице Excel (рис. 6, 6- а).
методом трапеций (8) выполним в таблице Excel (рис. 6, 6- а).
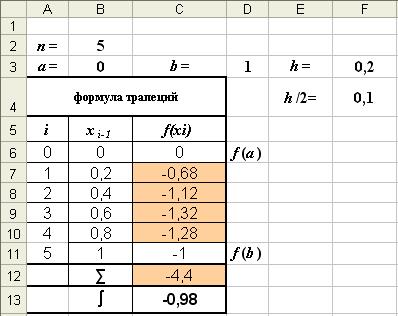
Режим решения
Рис. 6
∑ = -0,68 -1,12 -1,32 -1,28 = -4,4 I = 0,1·[(0-1)-2·4,4] = -0,98
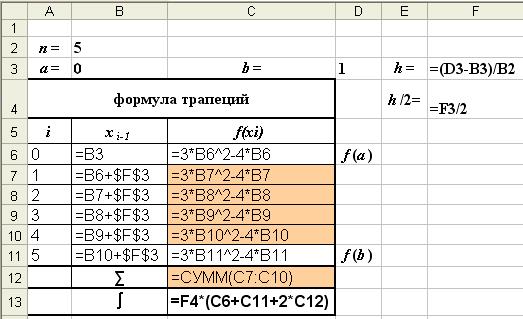
Режим показа формул
Рис. 6 - а
Разбивая интервал интегрирования на большее число отрезков, например, на 10, можно получить более точное решение (рис. 7).
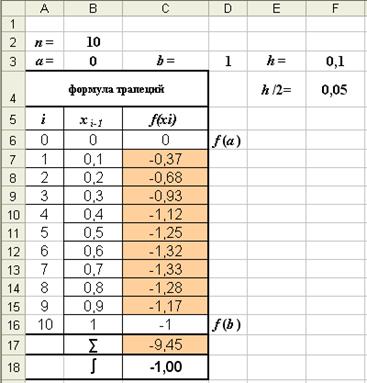
Рис. 7
|
 2015-10-22
2015-10-22 12249
12249
